Cho tam giác ABC, AD là phân giác của góc A, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song với AC, AB, chúng cắt AB, AC theo thứ tự ở P và Q. Chứng minh\(\frac{AP}{AB}+\frac{AQ}{AC}=1\)?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2016
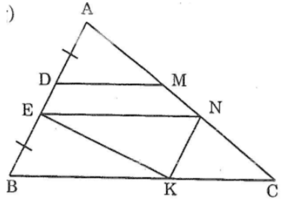
qua N kẻ đường thẳng song song với AB cắt BC tại K .
Vì EN song song với BK; NK song song với EB nên EB=NK;EN=BK (tính chất đoạn chắn)
nên NK=AD. Vì DM song song với BC nên góc( từ sau góc mình kí hiệu là >) DMA = >ACB . Vì NK song song với AB nên >A= >KNC \(\Rightarrow\) >B=>NKC Do đó ΔADM=ΔNKC (g.c.g). nên DM=KC
Suy ra DM+EN=BK+CK=BC(dpcm)
17 tháng 3 2020
Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )
CM
3 tháng 5 2019
Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.
Xét ΔBEK và Δ NKE, ta có:
∠(EKB) =∠(KEN) (so le trong vì EN // BC)
EK cạnh chung
∠(BEK) =∠(NKE) (so le trong vì NK // AB))
Suy ra: Δ BEK = Δ NKE(g.c.g)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét Δ ADM và Δ NKC, ta có:
∠A =∠(KNC) (đồng vị vì NK // AB)
AD = NK ( vì cùng bằng BE)
∠(ADM) =∠(NKC) (vì cùng bằng góc B)
Suy ra: Δ ADM = Δ NKC(g.c.g)
Suy ra: DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
đa phần mn ko bt cách tính =vv h tui sẽ cho cách giải
\(\text{Vì } QD \parallel AB,\text{ áp dụng định lý Talet, ta có: } \frac{AQ}{AC}=\frac{DC}{BC}(1)\)
\(\text{Vì } PD \parallel AC,\text{ áp dụng định lý Talet, ta có: } \frac{AP}{AB}=\frac{BD}{BC}(2)\)
\(\text{Từ (1), (2)} \implies \frac{AP}{AB} + \frac{AQ}{AC}=\frac{BD}{BC}+\frac{DC}{BC}=\frac{BC}{BC}=1 \text{ (đpcm)}\)
Vì PD // AB, áp dụng địng lý Talet, ta có: \(\frac{AP}{AB}=\frac{BD}{BC}\)(1)
Vì QD // AB, áp dụng định lý Talet, ta có: \(\frac{AQ}{AC}=\frac{DC}{BC}\)(2)
Từ (1), (2) => \(\frac{AP}{AB}+\frac{AQ}{AC}=\frac{BD}{BC}+\frac{DC}{BC}=\frac{BC}{BC}=1\left(đpcm\right)\)