Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
\(a,=\frac{2}{3}-\frac{16}{3}=\frac{-14}{3}\)
\(b,=\left(\frac{3}{7}+\frac{4}{7}\right)+\left(-\frac{6}{19}+\frac{-13}{19}\right)=1-1=0\)
\(c,=\frac{3}{5}.\left(\frac{8}{9}-\frac{7}{9}+\frac{26}{9}\right)=\frac{3}{5}.3=\frac{9}{5}\)
a,\(\dfrac{1}{2}\).\(\dfrac{4}{3}\)-\(\dfrac{20}{3}\).\(\dfrac{4}{5}\)=\(\dfrac{2}{3}\)-\(\dfrac{16}{3}\)=-\(\dfrac{14}{3}\)
a) = 1/2 + 1/3 = 5/6
b) = 2/5 + 2/3 = 16/15
c) = 7/11 . ( 3/4 + 1/4 ) + 4/11
= 7/11 . 1 + 4/11
= 7/11 + 4/11
= 1
d) = ( 3/4 + 1/2 + 1/4 ) . 8/3
= 3/2 . 8/3
= 4
1. \(A=\dfrac{2\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}{4\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}=\dfrac{2}{4}=\dfrac{1}{2}\)
2. \(B=\dfrac{1^2.2^2.3^2.4^2}{1.2^2.3^2.4^2.5}=\dfrac{1}{5}\)
3.\(C=\dfrac{2^2.3^2.\text{4^2.5^2}.5^2}{1.2^2.3^2.4^2.5.6^2}=\dfrac{125}{36}\)
4.D=\(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right).\dfrac{4}{9}.\dfrac{1}{16}=\dfrac{19}{30}.\dfrac{1}{36}=\dfrac{19}{1080}\)
Giải:
a) \(\dfrac{\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}-\dfrac{1}{6}}{-\left(\dfrac{4}{5}+\dfrac{1}{3}\right).\dfrac{1}{2}+1}=2\dfrac{33}{52}\)
\(\Leftrightarrow\dfrac{\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}-\dfrac{1}{6}}{-\dfrac{17}{15}.\dfrac{1}{2}+1}=\dfrac{137}{52}\)
\(\Leftrightarrow\dfrac{\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}-\dfrac{1}{6}}{\dfrac{13}{30}}=\dfrac{137}{52}\)
\(\Leftrightarrow\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}-\dfrac{1}{6}=\dfrac{137}{52}.\dfrac{13}{30}\)
\(\Leftrightarrow\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}-\dfrac{1}{6}=\dfrac{137}{120}\)
\(\Leftrightarrow\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}=\dfrac{137}{120}+\dfrac{1}{6}\)
\(\Leftrightarrow\left(x+\dfrac{3}{4}\right).\dfrac{7}{2}=\dfrac{157}{120}\)
\(\Leftrightarrow x+\dfrac{3}{4}=\dfrac{157}{120}:\dfrac{7}{2}\)
\(\Leftrightarrow x+\dfrac{3}{4}=\dfrac{157}{420}\)
\(\Leftrightarrow x=\dfrac{157}{420}-\dfrac{3}{4}\)
\(\Leftrightarrow x=-\dfrac{79}{210}\)
Vậy \(x=-\dfrac{79}{210}\).
b) \(\dfrac{\left(5-\dfrac{2}{7}\right).\dfrac{7}{9}.\dfrac{3}{5}}{\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}}=5\dfrac{5}{21}\)
\(\Leftrightarrow\dfrac{\left(5-\dfrac{2}{7}\right).\dfrac{7}{15}}{\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}}=\dfrac{110}{21}\)
\(\Leftrightarrow\dfrac{\dfrac{33}{7}.\dfrac{7}{15}}{\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}}=\dfrac{110}{21}\)
\(\Leftrightarrow\dfrac{\dfrac{11}{5}}{\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}}=\dfrac{110}{21}\)
\(\Leftrightarrow\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}=\dfrac{11}{5}:\dfrac{110}{21}\)
\(\Leftrightarrow\left(3x-\dfrac{5}{6}\right):\dfrac{1}{7}=\dfrac{21}{50}\)
\(\Leftrightarrow3x-\dfrac{5}{6}=\dfrac{21}{50}.\dfrac{1}{7}\)
\(\Leftrightarrow3x-\dfrac{5}{6}=\dfrac{3}{50}\)
\(\Leftrightarrow3x=\dfrac{3}{50}+\dfrac{5}{6}\)
\(\Leftrightarrow3x=\dfrac{67}{75}\)
\(\Leftrightarrow x=\dfrac{67}{75}:3\)
\(\Leftrightarrow x=\dfrac{67}{225}\)
Vậy \(x=\dfrac{67}{225}\).
Chúc bạn học tốt!
CÁC BẠN GIÚP MK NHA!!!
NGÀY MAI MK NỘP BÀI RỒI
AI TRẢ LỜI NHANH NHẤT
CHÍNH XÁC NHẤT VÀ RÕ RÀNG
THÌ MK TICK CHO NHA!!!
NHỚ TRẢ LỜI NHANH GIÙM MK NHA
a: =3/4-5/4+3/2x12/5=-1/2+36/10=-5/10+36/10=31/10
b: \(=\dfrac{-7}{13}\left(\dfrac{5}{9}+\dfrac{4}{9}\right)+\dfrac{7}{13}+8=8\)
\(Q=\dfrac{5}{11}.\dfrac{2}{17}+\dfrac{7}{17}.\dfrac{-6}{11}-\dfrac{9}{17}.\dfrac{5}{11}\)
\(Q=\dfrac{5}{11}\left(\dfrac{2}{17}-\dfrac{9}{17}\right)+\dfrac{7}{17}.\dfrac{-6}{11}\)
\(Q=\dfrac{5}{11}.\dfrac{-7}{17}+\dfrac{-7}{17}.\dfrac{6}{11}\)
\(Q=\dfrac{-7}{17}.\left(\dfrac{5}{11}+\dfrac{6}{11}\right)\)
\(Q=\dfrac{-7}{17}\)
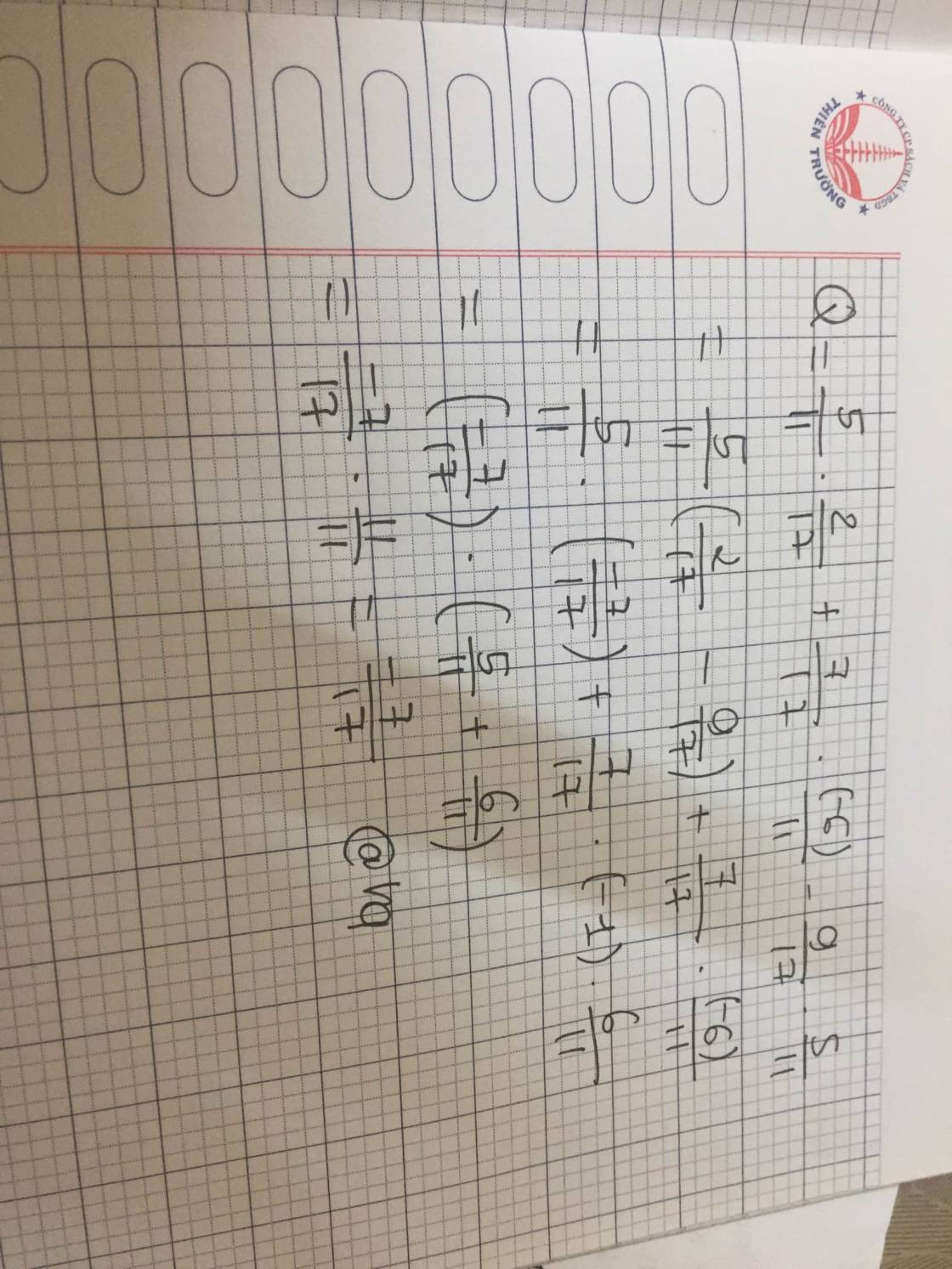
\(e.\dfrac{7}{10}\cdot\dfrac{-3}{5}+\dfrac{7}{10}\cdot\dfrac{-2}{5}-\dfrac{3}{10}\)
\(=\dfrac{7}{10}\cdot\left[\left(\dfrac{-3}{5}\right)+\left(\dfrac{-2}{5}\right)\right]-\dfrac{3}{10}\)
\(=\dfrac{7}{10}\cdot1-\dfrac{3}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
\(f.\dfrac{-3}{7}\cdot\dfrac{5}{9}+\dfrac{4}{9}\cdot\dfrac{-3}{7}+2\dfrac{3}{7}\)
\(=\dfrac{-3}{7}\cdot\left(\dfrac{5}{9}+\dfrac{4}{9}\right)+\dfrac{17}{3}\)
\(=\dfrac{-3}{7}\cdot1+\dfrac{17}{3}=\dfrac{-9}{21}+\dfrac{119}{21}=\dfrac{110}{21}\)
\(g.\dfrac{5}{9}\cdot\dfrac{10}{17}+\dfrac{5}{9}\cdot\dfrac{9}{17}-\dfrac{5}{9}\cdot\dfrac{2}{17}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{10}{17}+\dfrac{9}{17}-\dfrac{2}{17}\right)\)
\(=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)