Nếu |x| = 0,25 thì x2
Nhập kết quả dưới dạng phân số tối giản
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2016
\(\frac{9x}{4}=\frac{16}{x}\Rightarrow9x^2=36\Rightarrow x^2=4\Rightarrow x=\pm2\)
15 tháng 10 2016
9x2/4x = 64/4x
=>9x2=64
x2 = 64/9
x = 8/3 hoặc là (-8)/3
mà x là âm => x= (-8)/3
k cho a nha
5 tháng 6 2016
A chắc chắn phải dương, vì cả tử và mẫu đều cùng dấu dương.
Do đó khi 2A lớn nhất thì A cũng lớn nhất.
\(2A=\frac{2\left|x\right|+10}{2\left|x\right|+3}=1+\frac{7}{2\left|x\right|+3}\)
Để 2A lớn nhất thì \(\frac{7}{2\left|x\right|+3}\) lớn nhất. 7 là số nguyên dương nên để phân số này lớn nhất thì 2|x|+3 là số dương bé nhất có thể.
|x| > 0
\(\Rightarrow\)2|x| > 0
\(\Rightarrow\)2|x|+ 3 > 3
\(\Rightarrow2A\) lớn nhất là \(1+\frac{7}{3}=\frac{10}{3}\)
Do đó A lớn nhất là \(\frac{10}{3}:2=\frac{5}{3}\)
6 tháng 6 2016
Theo đẳng thức đề bài ta suy ra (7x + 2).(5x + 1) = (7x + 1).(5x + 7)
=> 7x.(5x + 1) + 2.(5x + 1) = 7x.(5x + 7) + 1.(5x + 7)
=> 35x2 + 7x + 10x + 2 = 35x2 + 49x + 5x + 7
=> 17x + 2 = 54x + 7
=> 54x - 17x = 7 - 2
=> 37x = 5
=> x = \(\frac{5}{37}\)
HP
6 tháng 6 2016
Theo t/c dãy tỉ số=nhau;
\(\frac{7x+2}{5x+7}=\frac{7x+1}{5x+1}=\frac{7x+2-\left(7x+1\right)}{5x+7-\left(5x+1\right)}=\frac{7x+2-7x-1}{5x+7-5x-1}=\frac{1}{6}\)
=>\(\frac{7x+2}{5x+7}=\frac{1}{6}\)
=>(7x+2).6=5x+7
=>42x+12=5x+7
=>42x+12-(5x+7)=0
=>42x+12-5x-7=0=>37x-5=0=>x=5/37
Vậy...
17 tháng 10 2017
Ta có: 4,1(2)= \(\frac{412-41}{90}\)=\(\frac{371}{90}\)
CM
29 tháng 4 2018
Gọi phân số tối giản phải tìm là a/b; (a; b ∈ Z; b ≠ 1), ƯCLN (a, b) = 1
Ta có a.b = 3150 = 2. 32. 52. 7 và a, b đều là ước của 3150.
Vì phân số này có thể viết được dưới dạng số thập phân hữu hạn nên b chỉ có ước nguyên tố là 2 và 5.
Do đó, b ∈ {2; 25; 50}.
- Với b = 2 thì a = 3150:2 = 1575
- Với b = 25 thì a = 3150:25 = 126
- Với b = 50 thì a = 3150:50 = 63
Vậy các phân số phải tìm là:
31 tháng 12 2016
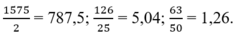
\(1,\left(23\right)=1+0,\left(23\right)=1+\frac{23}{99}=\frac{122}{99}\)
31 tháng 12 2016
\(1,\left(23\right)=1+0,\left(23\right)=1+\frac{23}{99}=\frac{99+23}{99}=\frac{122}{99}=\left(\frac{2.61}{3^2.11}\right)\) chi tiết hết cỡ rồi (chỉ để xem tối giản chưa thôi)
\(x^2=\left(\frac{1}{4}\right)^2=\frac{1^2}{4^2}=\frac{1}{16}\)
I x I = 0.25 => x=0.25 hoặc -0.25
TH1: x=0.25 => \(x^2=\frac{1}{16}\)
TH2: x=-0.25 => \(x^2=\frac{1}{16}\)
Vậy ..............