Một vật là hợp kim đồng và kẽm có khối lượng là 124 gam và có thể tích là 15cm3. Tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm, biết rằng cứ 89 gam đồng thì có thể tích là 10cm3 và 7 gam kẽm thì có thể tích là 1cm3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124

Thể tích của x (g) đồng là 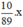 (
c
m
3
)
(
c
m
3
)
Thể tích của y (g) kẽm là 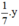 (
c
m
3
).
(
c
m
3
).
Vật có thể tích 15cm3 nên ta có phương trình: 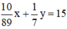
Ta có hệ phương trình:
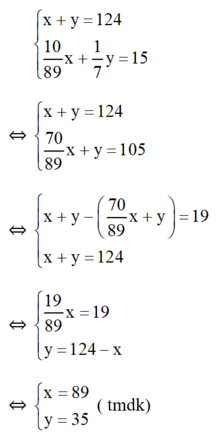
Vậy có 89 gam đồng và 35 gam kẽm.

Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124

Thể tích của x (g) đồng là 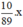 (cm3)
(cm3)
Thể tích của y (g) kẽm là 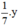 (cm3).
(cm3).
Vật có thể tích 15cm3 nên ta có phương trình: 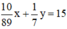
Ta có hệ phương trình:
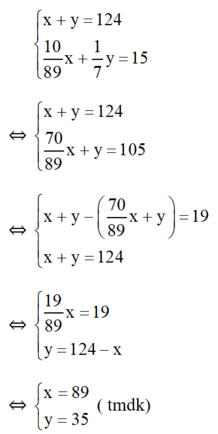
Vậy có 89 gam đồng và 35 gam kẽm.

Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
( Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124
89 gam đồng có thể tích \(10cm^3\)
=> 1 gam đồng có thể tích là \(\frac{10}{89}cm^3\)
7g kẽm có thể tích là \(1cm^3\)nên 1g kẽm có thể tích là \(\frac{1}{7}cm^3\)
Thể tích của x (g) đồng là \(\frac{10}{89}.x\left(cm^3\right)\)
Thể tích của y (g) kẽm là \(\frac{1}{7}.x\left(cm^3\right)\)
Vật có thể tích 15cm3 nên ta có phương trình \(\frac{10}{89}x+\frac{1}{7}y=15\)
Ta có hệ phương trình :
\(\hept{\begin{cases}x+y=124\\\frac{10}{89}x+\frac{1}{7}y=15\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y=124\\\frac{70}{89}x+y=105\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y-\left(\frac{70}{89}x+y\right)=19\\x+y=124\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{19}{89}x=19\\y=124-x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=89\\y=35\end{cases}\left(tmđk\right)}\)
Vậy có 89 gam đồng và 35 gam kẽm

Gọi khối lượng đồng trong hợp kim là x (0 < x < 124)
Ta có khối lượng kẽm trong hợp kim là 124 – x
Vì 89g đồng thì có thể tích là 10 c m 3 nên x (g) đồng có thể tích là 10x/89
7g kẽm thì có thể tích là 1 c m 3 nên 124 – x (g) kẽm có thể tích là (124-x)/7
Vì thể tích của hợp kim ban đầu là 15 c m 3 nên ta có phương trình:
10 x 89 + 124 - x 7 = 15 ⇔ −19x = −1691 ⇔ x = 89 (tmdk)
Vậy khối lượng đồng và kẽm trong hợp kim lần lượt là 89g và 35g
Đáp án: D

Khối lượng của hai thanh tỉ lệ theo hệ số tỉ lệ : 10/15
Gọi khối lượng hai thanh kim loại lần lượt là : x và y (gam)
⇒ x = 8,9 . 10 = 89 (gam)
y = 8,9 . 15 = 133,5 (gam)

Gọi m1 là khối lượng của chì, m2 là khối lượng của kẽm, m là khối lượng của hợp kim:
m = m1 + m2 = 0,05kg (1)
Nhiệt lượng chì và kẽm tỏa ra:
Q1 = m1.c1.(t0 - t) = m1.130.(136 – 18) = 15340.m1
Q2 = m2.c2.(t0 - t) = m2.210.(136 – 18) = 24780.m2
Nhiệt lượng nước thu vào:
Qn = mn.cn.(t - tn) = 0,05.4200.(18 - 14) = 810J
Vì muốn cho nhiệt lượng kế nóng thêm lên 1oC thì cần 65,1J nên nhiệt lượng kế thu vào:
Q4 = Qk.(t – tn) = 65,1.(18 – 14) = 260,4J
Vì nhiệt lượng tỏa ra bằng nhiệt lượng thu vào nên: Q3 + Q4 = Q1 + Q2
↔ 15340.m1 + 24780.m2 = 1100,4 (2)
Từ (1), rút m2 = 0,05 – m1, thay vào phương trình (2), giải ra ta được:
m1 = 0,015kg, suy ra m2 = 0,035kg
Vậy khối lượng chì là 15 gam và khối lượng kẽm là 35 gam.

Khối lượng của hai thanh tỉ lệ theo hệ số tỉ lệ : 10/15
Gọi khối lượng hai thanh kim loại lần lượt là : x và y (gam)
\(\frac{x}{y}\)\(=\frac{10}{15}\)\(=\frac{x}{10}\)\(=\frac{y}{15}\)và \(x+y=222,5\)
\(\frac{x}{10}\)\(=\frac{y}{15}\)\(=\frac{x+y}{10+15}\)\(=\frac{222.5}{25}\)\(=8,9\)
\(x=8,9.10=89\left(gam\right)\)
\(y=8,9.15=133,5\left(gam\right)\)