CMR: phương trình 4x2+4x=8y3-2z+4 không có nghiệm nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
NT
1
NV
1
3 tháng 1 2018
Xét x là số chẵn thì \(x^4⋮16\)
Xét x là số lẻ thì:
\(x^2:8\)dư 1
\(\Rightarrow x^4=\left(8k+1\right)^2:16\)dư 1
Như vậy mỗi số \(x^4;y^4;z^4;t^4\)chia cho 16 dư 1 hoặc 0
Nên \(x^4+y^4+z^4+t^4\)chia cho 16 có số dư không lớn hơn 5
Mà 2015 chia cho 16 dư 15
Dẫn đến mâu thuẫn
Hay x;y;z;t không tồn tại
Vậy phương trình không có nghiệm nguyên
CM
16 tháng 4 2019
Chọn D.
Đặt 
khi đó phương trình tương đương với: t2 - 6t + m – 3 = 0 (*)
Để phương trình đã cho có 4 nghiệm phân biệt khi (*) có 2 nghiệm dương phân biệt lớn hơn 1.
CM
11 tháng 10 2017
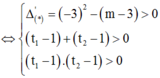
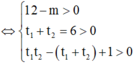
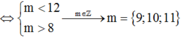
Điều kiện xác định x ∈ R
Đặt t = x 2 + 1 , t ≥ 1
Phương trình trở thành t 2 - 1 - 4 t - m + 1 = 0 ⇔ t 2 - 4 t = m 2
Để phương trình có 4 nghiệm phân biệt thì phương trình (2) có hai nghiệm phân biệt lớn hơn 1.
Xét hàm số f t = t 2 - 4 t có đồ thị là parabol có hoành độ đỉnh x = 2 ∈ 1 ; + ∞ nên ta có bảng biến thiên:
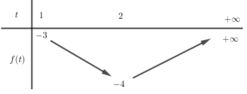
Dựa BBT ta thấy để (2) có hai nghiệm phân biệt lớn hơn 1 thì - 4 < m < - 3
Vậy không có giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: B
PT
1
4x2+4x=8y3-2z+4
<=> 2x2+2x=4y3-z+2
<=>2x(x+1)=4y3-2z+2
Ta có : VT chia hết cho 4 =>VP chia hết cho 4 , 4y3 chia hết cho 4
2z chia hết cho 4 => z chia hết cho 2 , mà 2 ko chia hết cho 2 => pt trên không có No nguyên