Đề bài:
Có 6 chữ số 1, 2, 3, 4, 5, 6.
Mỗi chữ số được dùng 1 lần.
Hãy lập ra 2 số có 3 chữ số sao cho hiệu giữa số lớn hơn và số nhỏ hơn là nhỏ nhất có thể.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 2 số đó là "abc" ; "def" trong đó ("abc">"def")
Để hiệu 2 số đó bé nhất thì thỏa mãn 2 điều kiện sau:
- a,d là 2 số liên tiếp (2;1), (3;2), (4;3), (5;4), (6;5)
- "bc" bé nhất là "ef" lớn nhất => "bc" = 12; "ef"= 65
=> (a;d)=(4;3)
Vậy 2 số đó là 412 và 365.

Ta có:
abc - def (a >d)
Đế hiệu giữa số lớn hơn và số nhỏ hơn là nhỏ nhất có thể thì a phải hơn d ít nhất 1 đơn vị. ef > bc sao cho ef lớn nhất có thể và bc phải nhỏ nhất cỏ thể.
Ta chọn a = 4 thì d = 3
Ta chỉ còn 4 số : 1 ; 2 ; 5 ; 6.
mà ab nhỏ nhất có thể nên ab = 12
và ef lớn nhất co thể nên ef = 65.
Vậy hiệu giữa số lớn hơn và số bé hơn là nhỏ nhất có thể sẽ là : 412 - 365 = 47.

Tổng 3 chữ số đầu và 3 chữ số cuối là 2+3+4+5+6+7=27, hiệu của chúng là 3
\(\Rightarrow\) Tổng 3 chữ số đầu là 12
\(\Rightarrow\) 3 chữ số đầu là (2;3;7); (2;4;6);(3;4;5) có 3 trường hợp (với mỗi bộ 3 chữ số đầu sẽ có đúng 1 bộ 3 chữ số cuối tương ứng)
\(\Rightarrow\) Có \(3.3!.3!=108\) số thỏa mãn

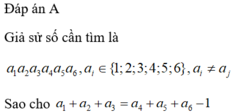
![]()
![]()
![]()
![]()
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: ![]()
Gọi 2 số đó là "abc" ; "def" trong đó ("abc">"def")
Để hiệu 2 số đó bé nhất thì thỏa mãn 2 điều kiện sau:
- a,d là 2 số liên tiếp (2;1), (3;2), (4;3), (5;4), (6;5)
- "bc" bé nhất là "ef" lớn nhất => "bc" = 12; "ef"= 65
=> (a;d)=(4;3)
Vậy 2 số đó là 412 và 365.
2 số đó là :
123 , 124