Cho hình thang ABCD (AB//CD). 2 đường chéo cắt nhau tạo O và góc DOC = 60o
a) chứng minh tam giác DOC,tam giác AOB là tam giác đều
b)Gọi M,N,K là trung điểm của OA,OD,BC.Chứng minh tam giác MNK là tam giác đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
CM
3 tháng 3 2019
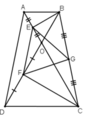
ΔAOB đều ⇒ BE là đường trung tuyến đồng thời là đường cao
⇒ BE ⊥ AO
⇒ ΔBEC vuông tại E
Mà EG là đường trung tuyến
⇒ 
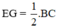(1)
ΔCOD đều ⇒ CF là đường trung tuyến đồng thời là đường cao
⇒ CF ⊥ OD
⇒ ΔBFC vuông tại F
Mà FG là đường trung tuyến
⇒ 
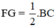(2)
Hình thang ABCD (AB// CD) có: AC = AO + OC = OB + OD = BD
⇒ ABCD là hình thang cân
⇒ AD = BC.
ΔAOD có: AE = EO, FO = FD
⇒ EF là đường trung bình của ΔAOD
⇒ 
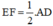
Mà AD = BC (cmt)
⇒ 
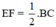(3)
Từ (1); (2); (3) suy ra EF = FG = GE ⇒ ΔEFG đều (đpcm).
21 tháng 9 2017
2 đường chéo AC; BD cắt nhau tại O. Do hình thang ABCD cân (AB//CD)
=> OA=OB; OC=OD (Tự chứng minh)
Mà ^AOB=600 => ^COD=600 (Đối đỉnh) => Tam giác AOB và tam giác COD đều.
Xét tam giác AOB đều: H là trung điểm OA => BH vuông góc OA
=> Tam giác BHC vuông tại H; K là trung điểm của BC => HK=BK=CK=BC/2 (1)
Tương tự: Tam giác CIB vuông tại I, K là trung điểm BC => IK=CK=BK=BC/2 (2)
Xét tam giác AOD: H là trung điểm OA; I là trung điểm OD => IH là đường trung bình tam giác AOD.
=> IH=AD/2. Mà hình thang ABCD cân (AB//CD) => AD=BC => IH=BC/2 (3)
Từ (1); (2) và (3) => HK=IK=IH => Tam giác HIK là tam giác đều (đpcm).
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
