Hai đội công nhân đào chung con mương trong 10 ngày sẽ hoàn thành. Họ làm chung với nhau được 6 ngày thì đội I được điều động đi chỗ khác. Với tinh thần thi đua, đội II làm với năng suất gấp đôi nên s...

Y

Yeogeol_angg

13 tháng 3 2022

Hai đội công nhân đào chung con mương trong 10 ngày sẽ hoàn thành. Họ làm chung với nhau được 6 ngày thì đội I được điều động đi chỗ khác. Với tinh thần thi đua, đội II làm với năng suất gấp đôi nên sau 3 ngày nữa đã đào xong con mương. Hỏi nếu mỗi đội làm một mình thì phải mất bao lâu mới đào xong...

Đọc tiếp

#Toán lớp 9

0

P

PUBGM̃̃̃̃̃̃̃̃̉̃̉̃̃̃́̃̃̃́̃́̃̀̉́́́́́́...

23 tháng 3 2022

Bài 3:Hai đội công nhân đào chung một con mương trong 10 ngày sẽ hoàn thành. Họ làm chung với nhau được 6 ngày thì đội I được điều đi chỗ khác. Với tinh thần thi đua, đội II làm với năng suất gấp đôi nên sau 3 ngày nữa đó đào xong con mương. Tính thời gian mỗi đội đào một mình xong con...

Đọc tiếp

#Toán lớp 9

0

LM

Lê Minh Ngọc

3 tháng 5 2021

Hai đội thanh niên xung kích cùng đào chung một con mương và dự định trong 10 ngày sẽ hoàn thành . Họ làm chung với nhau được 6 ngày thì một đội được điều động đi làm chỗ khác . Nhưng với tinh thần thi đua , đội còn lại làm với năng suất gấp đôi nên chỉ sau 3 ngày nữa đã đào xong con mương . Hỏi nếu làm một mình thì mỗi đội phải mất bao nhiêu ngày mới đào xong con...

Đọc tiếp

#Toán lớp 9

2

MY

missing you =

3 tháng 5 2021

gọi x,y là số ngày mà đội 1 , đội 2 làm một mình xong con mương(x,y>10)

trong 1 ngày đội 1 làm được 1/x(công việc)

trong 1 ngày đội 2 làm được 1/y(công việc)

vì 2 đội làm chung theo dự định trong 10 ngày hoàn thành

nên trong 1 ngày 2 đội làm chung được 1/10(công việc)

=> pt: 1/x+1/y=1/10(1)

vì 2 đội làm chung với nhau được 6 ngày nên cả 2 đội làm được 6/10(công việc)=3/5(công việc)

nên số công việc còn lại là 100%-3/5=1-3/5=2/5(công việc)

vì đội 1 được điều động đi chỗ khác và đội 2 làm công việc với năng suất gấp đôi nên sau 3 ngày hoàn thành công việc

=>pt:3.2.1/y=2/5=6.1/y=2/5

từ (1)(2) (tự giải hệ pt)=>x=30(TM),y=15(TM)

VẬy nếu làm riêng thì đội 1 mất 30 ngày,đội 2 mất 15 ngày

Đúng(1)

SC

Slena Christina

7 tháng 3 2022

Gọi thời gian đội 1 làm một mình xong cv là x (x>10; ngày)

thời gian đội 2 làm một mình xong cv là y (y>10; ngày)

Đội 1 làm một mình được $\dfrac{1}{x}$(công việc)

Đội 2 làm một mình được $\dfrac{1}{y}$(công việc)

Vì 2 đội đào chung con mương trong 10 ngày thì hoàn thành

=> 1 ngày 2 đội làm chung được $\dfrac{1}{10}$(cv)

=> $\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\left(1\right)$

Vì 2 đội làm chung với nhau được 6 ngày => cả 2 đội làm được $\dfrac{6}{10}\left(cv\right)=\dfrac{3}{5}\left(cv\right)$

=> số công việc còn lại là: $1-\dfrac{3}{5}=\dfrac{2}{5}\left(cv\right)$

Vì đội 1 được điều động đi chỗ khác và đội 2 làm công việc với năng suất gấp đôi nên sau 3 ngày hoàn thành cv

=> $\dfrac{3.2.1}{y}=\dfrac{2}{5}\Leftrightarrow\dfrac{6}{y}=\dfrac{2}{5}\left(2\right)$

Từ (1)(2) => hpt: $\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\\\dfrac{6}{y}=\dfrac{2}{5}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}y=\left(6.5\right):2\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}+\dfrac{1}{15}=\dfrac{1}{10}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{10}-\dfrac{1}{15}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{30}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}x=30\left(TM\right)\\y=15\left(TM\right)\end{matrix}\right.$

Vậy đội 1 làm một mình trong 30 ngày thì mới đào xong mương

đội 2 làm một mình trong 15 ngày thì mới đào xong mương

Đúng(0)

PT

Pham Trong Bach

20 tháng 10 2018

Hai đội xây dựng làm chung một công việc và dự định hoàn thành trong 12 ngày. Nhưng khi làm chung được 8 ngày thì đội I được điều động đi làm việc khác. Tuy chỉ còn một mình độ II làm việc nhưng do cải tiến cách làm, năng suất của đội II tăng gấp đôi nên họ làm xong phần việc còn lại trong 3,5 ngày. Hỏi với năng suất ban đầu, nếu mỗi đội làm một mình thì phải làm trong bao nhiêu...

Đọc tiếp

#Toán lớp 9

1

CM

Cao Minh Tâm

20 tháng 10 2018

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)

Điều kiện : x, y > 12, x,y ∈ N.

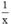Một ngày đội I làm được : Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 (công việc).

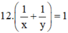
Một ngày đội II làm được : Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 (công việc).

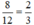+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9

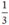+ Hai đội cùng làm trong 8 ngày được: Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

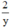⇒ còn lại đội II phải hoàn thành một mình Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

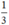Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

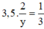
Đội II hoàn thành Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc còn lại trong 3,5 ngày nên ta có phương trình:

Ta có hệ phương trình:

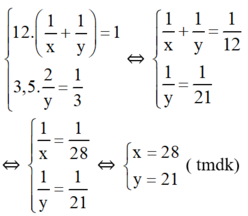
Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Đúng(0)

PT

Pham Trong Bach

4 tháng 7 2019

Hai đội xây dựng làm chung một công việc và dự định hoàn thành trong 12 ngày. Nhưng khi làm chung được 8 ngày thì đội I được điều động đi làm việc khác. Tuy chỉ còn một mình độ II làm việc nhưng do cải tiến cách làm, năng suất của đội II tăng gấp đôi nên họ làm xong phần việc còn lại trong 3,5 ngày. Hỏi với năng suất ban đầu, nếu mỗi đội làm một mình thì phải làm trong bao nhiêu...

Đọc tiếp

#Toán lớp 9

1

CM

Cao Minh Tâm

4 tháng 7 2019

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)

Điều kiện : x, y > 12, x,y ∈ N.

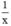Một ngày đội I làm được : Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 (công việc).

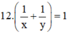
Một ngày đội II làm được : Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 (công việc).

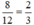+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9

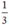+ Hai đội cùng làm trong 8 ngày được: Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

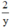⇒ còn lại đội II phải hoàn thành một mình Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

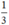Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc.

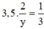
Đội II hoàn thành Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9 công việc còn lại trong 3,5 ngày nên ta có phương trình:

Ta có hệ phương trình:

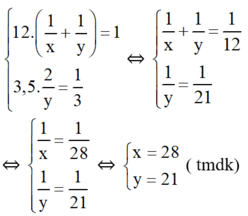
Giải bài 45 trang 27 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Đúng(1)

AA

Admin (a@olm.vn)

Admin VIP

21 tháng 3 2021 - olm

Hai đội xây dựng cùng làm chung một công việc và dự định hoàn thành sau 12 ngày. Họ cùng làm chung với nhau được 8 ngày thì đội 1 được điều động đi làm việc khác, đội 2 tiếp tục làm. Do cải tiến kĩ thuật, năng suất tăng gấp đôi nên đội 2 đã hoàn thành công việc sau 3,5 ngày. Hỏi mỗi đội làm một mình thì sau bao nhiêu ngày sẽ xong công việc?

#Toán lớp 9

3

JF

Ĵ❍ƙĔŔᵛᶰ(*•.¸♡ţęąɱ ƒŗęę ƒįŗę❤☆)

21 tháng 3 2021

Gọi $x$ (ngày) là thời gian đội I làm một mình xong công việc với năng suất ban đầu $(x > 0)$ ,

$y$ (ngày) là thời gian đội II làm một mình xong công việc với năng suất ban đầu $(y > 0)$

Trong 1 ngày đội I làm được $\frac{1}{x}$ (công việc),

đội II làm được $\frac{1}{y}$ (công việc)

Hai đội xây dựng làm chung theo dự định trong 12 ngày xong nên ta có:

$12. \frac{1}{x} + 12. \frac{1}{y} = 1$ (1)

Cả hai đội làm chung 8 ngày thì được $\frac{8}{12} = \frac{2}{3}$ (công việc)

Số công việc còn lại của đội II làm là: $1 - \frac{2}{3} = \frac{1}{3}$ (công việc)

Năng suất của đội II tăng gấp 2 lần nên 1 ngày làm được $2 \cdot \frac{1}{y} = \frac{2}{y}$ công việc

Khi năng suất tăng họ làm 3,5 ngày thì hoàn thành phần công việc còn lại nên ta có:

$3, 5. \frac{2}{y} = \frac{1}{3} \Rightarrow y = 21$ (2)

Thay vào (1) suy ra $12. \frac{1}{x} + 12. \frac{1}{21} = 1 \Rightarrow x = 28$

Vậy nếu làm theo dự định thời gian đội I làm một mình xong công việc là $28$ ngày, thời gian đội II làm một mình xong công việc là $21$ ngày.

Đúng(0)

HD

Hồ Đức Việt

21 tháng 3 2021

Gọi x,y theo thứ tư là thời gian mà mỗi đội làm một mình thì hoàn thành công việc.

Với năng suất ban đầu: x,y > 0 và tính theo đơn vị ngày.

Trong 1 ngày đội I làm được 1/x công việc. 1 ngày đội II làm được 1/y công việc. 1 ngày cả 2 đội làm được 1/12 công việc.

Ta có phương trình: 1/x + 1/y = 1/12 (công việc)( 1)

Trong 8 ngày cả hai đội làm được 8. 1/12 = 2/3 (công việc).

Sau khi một đội nghỉ, năng suất của đội II là 2/y. Họ phải làm trong 3,5 ngày thì xong công việc nên ta có phương trình 1/3 : 2/y = 7/2

(2)

Ta có hệ:Giải hệ1,2 này, ta được x = 28 (ngày); y = 21(ngày) Chú ý: Ta có thể đặt hệ

Đúng(0)

JJ

jinjin jinjin

27 tháng 7 2021

Hai đội công nhân cùng làm chung một con đường và dự định 10 ngày sẽ xong. Họ làm chung với nhau được 6 ngày thì đội I nghỉ làm. Đội II làm một mình nên đã cố gắng tăng nâng suất gấp đôi nên chỉ sau 3 ngày sau là làm xong cong đường. Hỏi nếu mỗi đội làm một mình thì mất bao lâu mới làm xong con đường.ko giải theo hệ phương...

Đọc tiếp

#Toán lớp 8

0

NP

Nguyễn Phương Anh

23 tháng 3 2021 - olm

Hai đội công nhân cùng làm một con đường và dự định 10 ngày sẽ xong. Họ làm chung với nhau được 6 ngày thì đội I nghỉ làm. Đội II làm một mình nên đã cố gắng tăng năng suất gấp đôi nên chỉ sau 3 ngày là làm xong con đường. Hỏi nếu mỗi đội làm 1 mình thì mất bao lâu mới làm xong con đường.

#Toán lớp 8

7

NT

nguyễn tiên dũng

23 tháng 3 2021

trần thị tương vy anh yêu em

Đúng(0)

TD

Trần Diệu Thảo Linh

23 tháng 3 2021

CẤM PHÁT CƠM CHÓ DƯỚI MỌI HÌNH THỨC

Đúng(0)

PT

Phan Thị Thu Hiền

7 tháng 4 2023 - olm

Hai đội công nhân cùng làm chung 1 công việc trong 12 ngày thì xong . Khi làm chung được 8 ngày thì đội 1 được điều động đi làm việc khác ,đội thứ 2 tiếp tục làm việc với năng suất gấp đôi , do đó đội 2 đã hoàn thành phần việc còn lại trong 8 ngày tiếp theo . Hỏi với năng suất ban đầu thì mỗi đội làm một mình sẽ hoàn thành công việc đó trong bao...

Đọc tiếp

#Toán lớp 9

0

M

Misaka

12 tháng 8 2015 - olm

hai đội xây dựng cùng làm chung 1 công việc và dự định trong 12 ngày thì xog. Họ cùng làm với nhau 8 ngày thì đội I được điều động làm việc khác,đội II tiếp tục làm.Do cải tiến kĩ thuật ,năng suất tăng gấp đôi nên đội II làm xog phần việc còn lại trog 3 ngày rưỡi.Hỏi nếu mỗi đội làm một mình thì bao nhiêu ngày xog công việc trên?

#Toán lớp 8

1

HH

Huy Hoang

1 tháng 10 2020

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y ( ngày )

Điều kiện : $x,y>12 ; x,y\in N$

Một ngày đội I làm được : $\frac{1}{x}$công việc

Một ngày đội II làm được : $\frac{1}{y}$công việc

+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình : $12.\left(\frac{1}{x}+\frac{1}{y}\right)=1$

+ Hai đội cùng làm trong 8 ngày được : $\frac{8}{12}=\frac{2}{3}$công việc

=> Còn lại đội II phải hoàn thành một mình $\frac{1}{3}$công việc

Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được $\frac{2}{y}$công việc

Đội II hoàn thành $\frac{1}{3}$công việc còn lại trong 3,5 ngày nên ta có PT : $3,5.\frac{2}{y}=\frac{1}{3}$

Ta có HPT : $\hept{\begin{cases}12.\left(\frac{1}{x}+\frac{1}{y}\right)=1\\3,5.\frac{2}{y}=\frac{1}{3}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\\frac{1}{y}=\frac{1}{21}\end{cases}}}$

$\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{28}\\\frac{1}{y}=\frac{1}{21}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=28\\y=21\end{cases}\left(tmđk\right)}$

Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP