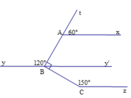
Cho hình vẽ bên .Tìm a để Ax//By 3a a B A x y ...
Đọc tiếp
Cho hình vẽ bên .Tìm a để Ax//By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 6 2018
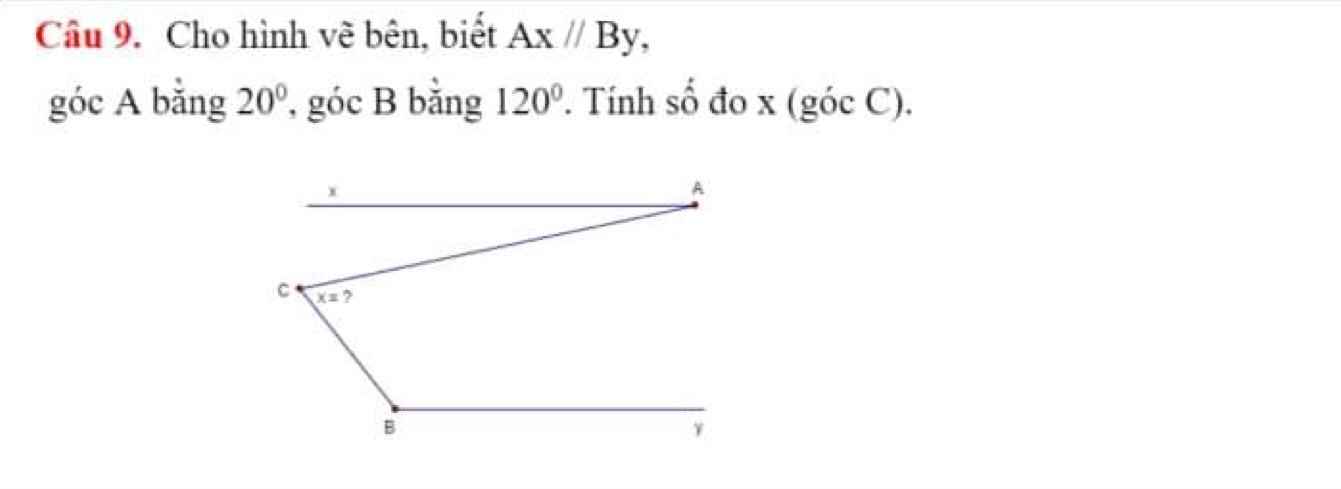
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
CM
25 tháng 8 2018
Đáp án C
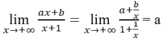
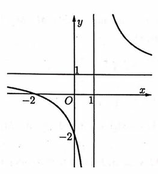
=> y = a là tiệm cận ngang.
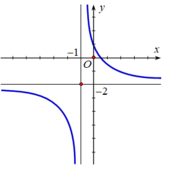
Dựa vào đồ thị hàm số có đường thẳng y = -2 là đường tiệm cận ngang nên a = -2
Mà đồ thị hàm số đi qua điểm (0; 1) nên b = 1
CM
18 tháng 2 2019
Chọn C.
Đồ thị hàm số có tiệm cận đứng là x=b=1, tiệm cận ngang là y=a=1.
CC
0
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
5 tháng 12 2021
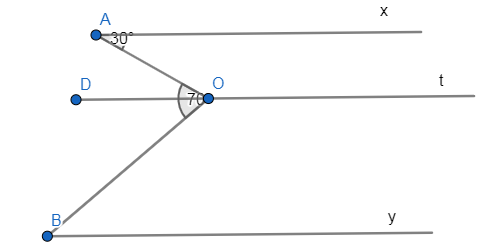
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
nha bạn chúc bạn học tốt