Bài 5: (3,5 điểm) Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm.
a) Tính BC.
b) Kéo dài AB lấy D sao cho B là trung điểm của AD. Nối CD, qua B vẽ đường thẳng vuông góc với AD cắt CD tại E. Chứng minh ΔABE = ΔDBE và suy ra ΔAED cân.
c) Kẻ AK vuông góc với BC tại K. Qua D kẻ đường thẳng vuông góc với đường thẳng CB tại F. Chứng minh B là trung điểm của KF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=13cm
b: Xét ΔABE vuông tại B và ΔDBE vuông tại B có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE
Suy ra: EA=ED
hay ΔEAD cân tại E
c: Xét ΔAKB vuông tại K và ΔDFB vuông tại F có
BA=BD
\(\widehat{ABK}=\widehat{DBF}\)
Do đó: ΔAKB=ΔDFB
Suy ra: BK=BF
hay B là trung điểm của KF

a: BC=13cm
b: Xét ΔABE vuông tại B và ΔDBE vuông tại B có
BA=BD
BE chung
Do đó: ΔABE=ΔDBE
Suy ra: AE=DE
hay ΔAED cân tai E

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay \(BC=13cm\)
Vậy: BC=13cm
b) XÉT ΔABE VÀ ΔDBE ,CÓ
BD=BA (B LÀ TRUNG ĐIỂM CỦA AD)
\(\widehat{DBE}=\widehat{ABE}\) =90
EB : CẠNH CHUNG
⇒ΔABE = ΔDBE (C-G-C)

Bạn tự vẽ hình nha.
a, Áp dụng Đ. L. py-ta-go vào tg ABC vuông tại A, có:
BC2=AC2+AB2
=>BC2=122+52
=144+25
=169.
=>BC=13cm.
b, Xét tg ABE và tg DBE, có:
BE chung
góc DBE= góc ABE(=90o)
AB=BD(B là trung điểm của AD)
=>tg DBE= tg ABE(2 cạnh góc vuông)
=>AD=ED(2 cạnh tương ứng)
=>tg ADE là tg cân tại E.
c, Xét tg BDF và tg BKA, có:
góc BDF= góc ABK(2 góc đối đỉnh)
DB=BD(B là trung điểm của AD)
góc DFB= góc BKA(=90o)
=>tg DFB= tg AKB(ch-gn)
=>FB=BK(2 cạnh tương ứng)
=>B là trung điểm của KF.
d, Ta có: góc DBE= góc ABE. Mà 2 tg AEB và tg DEB bằng nhau.
=>EB là tia phân giác của góc DEA.
Vì góc DAC= góc DBE(=90o) và 2 góc này ở vị trí đồng vị, suy ra:
BE // AC.
=>góc DEB= góc ECA( đồng vị)
=> góc BEA= góc EAC(SLT)
Mà góc DEB= góc BEA(BE là tia phân giác của góc DEA)
=>góc EAC= góc ECA.
=>tg AEC là tg cân tại E.
=>AE=EC.
Ta có: DE=EA(2 cạnh tương ứng)
AE=EC(cmt)
=>DE=EC.
=>E là trung điểm của DC(đpcm)

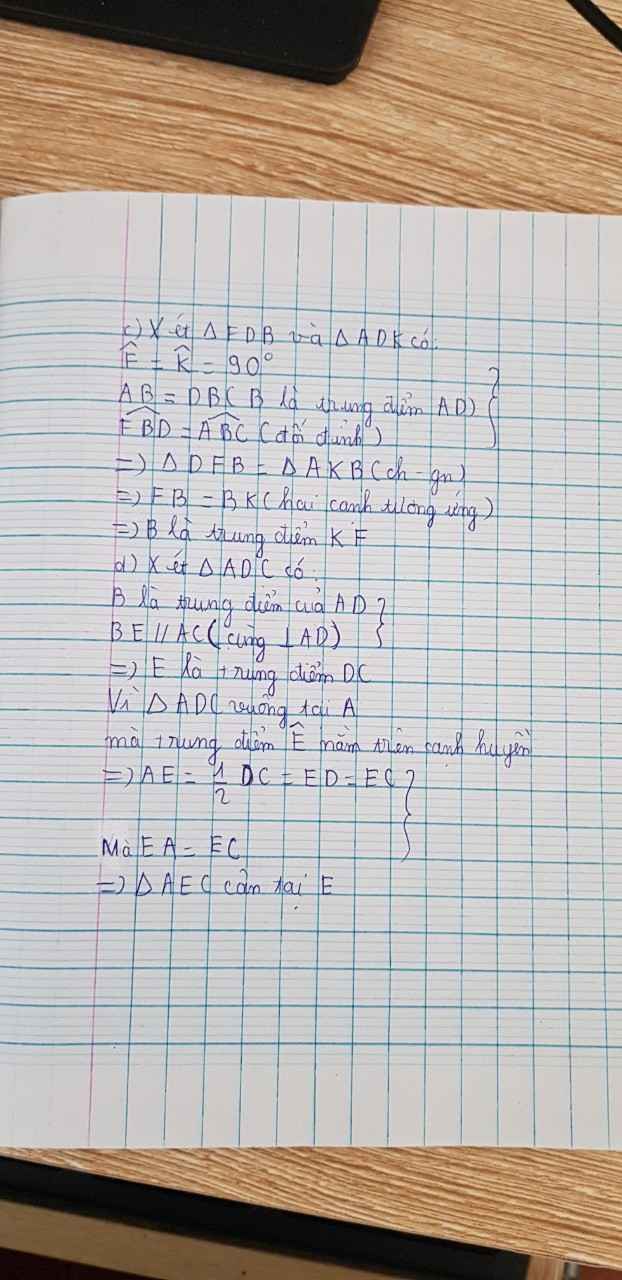

Bài 5:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
Vậy: BC=13cm
b) Xét ΔABE vuông tại B và ΔDBE vuông tại B có
EB chung
BA=BD(B là trung điểm của AD)
Do đó: ΔABE=ΔDBE(hai cạnh góc vuông)
Suy ra: EA=ED(Hai cạnh tương ứng)
Xét ΔEAD có EA=ED(cmt)
nên ΔEAD cân tại E(Định nghĩa tam giác cân)
Cái định lý pytago ấy kq = 179 mà sao lại = 169?