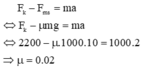Bài 1. Một xe tải 4 tấn đang chuyển động thẳng đều trên đường. Biết hệ số ma sát giữa xe và mặt đường là 0,04. Lấy g = 10 m/s2. Tính công của lực kéo động cơ giúp xe tải đi được quãng đường 0,4 km.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
☆Châuuu~~~(๑╹ω╹๑ )☆
12 tháng 3 2022
Đúng(0)
Những câu hỏi liên quan
6 tháng 2 2022
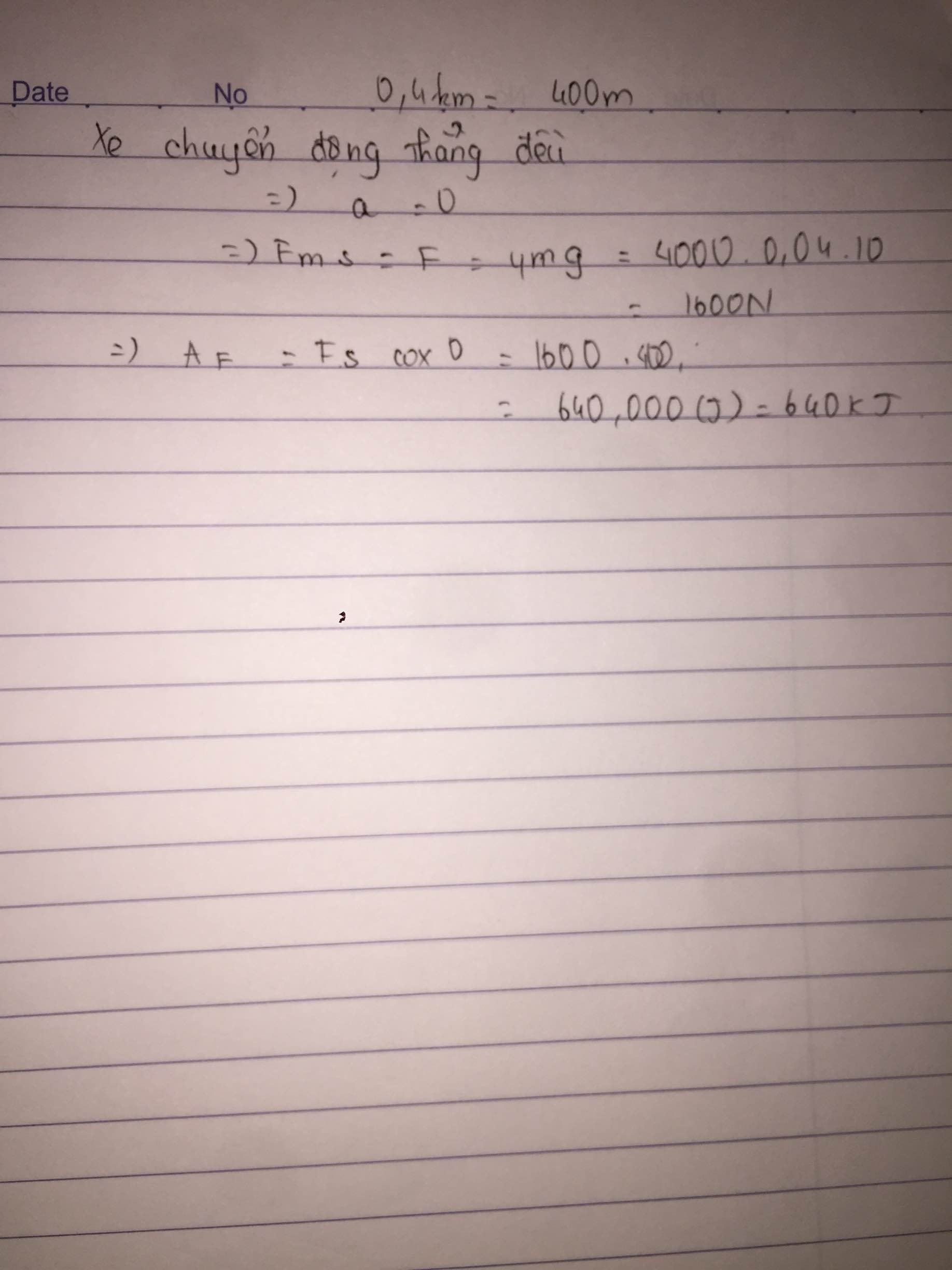
Công của lực ma sát:
\(A=-F_{ms}\cdot s=-a\cdot m\cdot g\cdot s=-0,04\cdot2\cdot1000\cdot10\cdot18=-14400J\)
N
28 tháng 11 2021
a. Chiếu theo ptr chuyển động:
\(-F_{ms}+F_k=ma\)
\(\Rightarrow F_k=ma+F_{ms}=ma+\mu mg=1000\cdot2+0,1\cdot1000\cdot10=3000\left(N\right)\)
b. Chiếu theo ptr chuyển động:
Khi xe chuyển động thẳng đều thì \(a=0\)
\(-F_{ms}+F_k=0\)
\(\Rightarrow F_k=F_{ms}=\mu N=\mu P=\mu mg=0,1\cdot1000\cdot10=1000\left(N\right)\)
10 tháng 2 2022
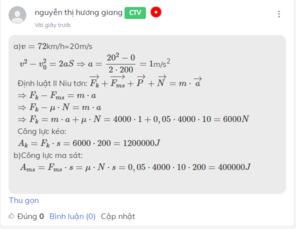
a)\(v=72\)km/h=20m/s
\(v^2-v^2_0=2aS\Rightarrow a=\dfrac{20^2-0}{2\cdot200}=1\)m/s2
Định luật ll Niu tơn: \(\overrightarrow{F_k}+\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F_k-F_{ms}=m\cdot a\)
\(\Rightarrow F_k-\mu\cdot N=m\cdot a\)
\(\Rightarrow F_k=m\cdot a+\mu\cdot N=4000\cdot1+0,05\cdot4000\cdot10=6000N\)
Công lực kéo:
\(A_k=F_k\cdot s=6000\cdot200=1200000J\)
b)Công lực ma sát:
\(A_{ms}=F_{ms}\cdot s=\mu\cdot N\cdot s=0,05\cdot4000\cdot10\cdot200=400000J\)
21 tháng 11 2021
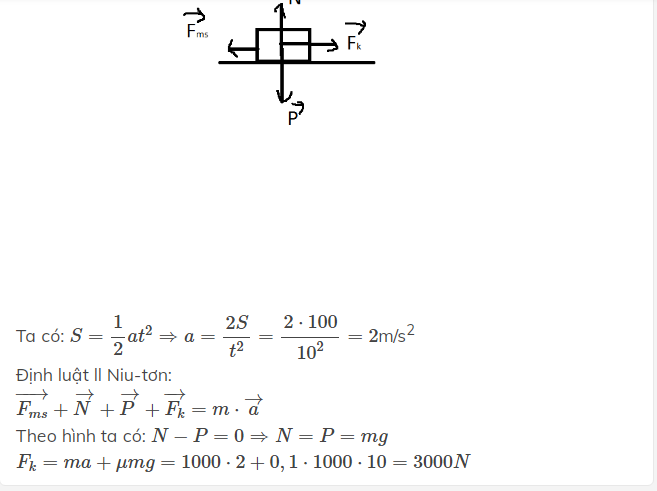
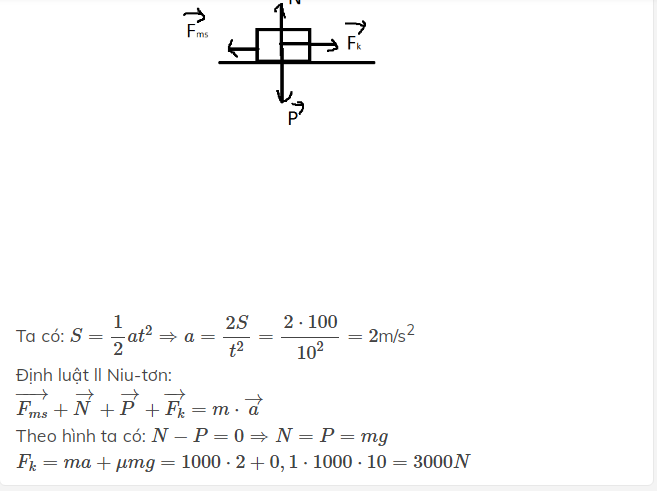
Ta có: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot100}{10^2}=2\)m/s2
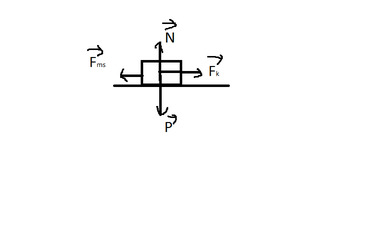
Định luật ll Niu-tơn:
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_k}=m\cdot\overrightarrow{a}\)
Theo hình ta có: \(N-P=0\Rightarrow N=P=mg\)
\(F_k=ma+\mu mg=1000\cdot2+0,1\cdot1000\cdot10=3000N\)
VT
31 tháng 12 2019
a/ (0,5 điểm)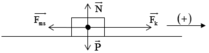 
b/ (0,5 điểm)
Gia tốc: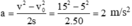 
c/ (1,0 điểm)
Áp dụng định luật II Niu – tơn: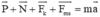 
Chiếu lên chiều dương (hoặc chiếu lên chiều chuyển động)
