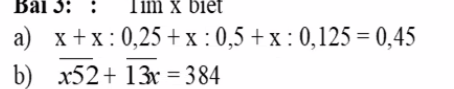
giúp mình với ạ.Mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
0
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Cộng 3 PT lại ta có:
$x(a+b+c)+y(a+b+c)=a+b+c$
$\Leftrightarrow (a+b+c)(x+y-1)=0$
$\Rightarrow a+b+c=0$ hoặc $x+y-1=0$
TH1: $a+b+c=0\Leftrightarrow a+b=-c$
Khi đó: $a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=3abc$
$\Rightarrow \frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=3$ (đpcm)
TH2: $x+y-1=0\Leftrightarrow y=1-x$
Thay vô hpt \(\left\{\begin{matrix} ax+b(1-x)=c\\ bx+c(1-x)=a\\ cx+a(1-x)=b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x(a-b)=c-b\\ x(b-c)=a-c\\ x(c-a)=b-a\end{matrix}\right.\)
\(\Rightarrow x^3(a-b)(b-c)(c-a)=(c-b)(a-c)(b-a)=-(a-b)(b-c)(c-a)\)
\(\Leftrightarrow (a-b)(b-c)(c-a)(x^3+1)=0\)
Nếu $a-b=0$ thì kéo theo $b-c=c-a=0$
$\Rightarrow a=b=c$
Nếu $b-c=0; c-a=0$ thì tương tự
Nếu $x^3+1=0\Leftrightarrow x=-1$
$\Rightarrow b-a=c-b=a-c\Rightarrow a=b=c$
Tóm lại $a=b=c$
Do đó: $\frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=1+1+1=3$ (đpcm)
PT
12 tháng 10 2021
Tham khảo
Không thể có tình bạn một phía để xây dựng một tình bạn trong sáng, lành mạnh phải có thiện chí và cố gắng từ cả hai phía.
2,43 gio
ở đâu đấy