Cho hình thoi ABCD. M là trung điểm của BC. Trên AM lấy E sao cho ∠ABE ∠CAM . CMRa, ▵DAE∞▵AMB đồng dạng nha mấy bạn b,∠MED ∠BCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 5 2023
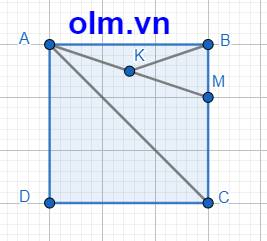
SABCD = 12 \(\times\)12 = 144 (cm2)
SABC = 12 \(\times\) 12 : 2 = 72 (cm2)
BM = 12 \(\times\) \(\dfrac{2}{3}\) = 8 (cm)
CM = 12 - 8 = 4 (cm)
SACM = 12 \(\times\)4 : 2 = 24 (cm2)
b, SABK = \(\dfrac{1}{2}\)SABM (vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáy BM và AK = \(\dfrac{1}{2}\)AM)
SABM = SABC - SAMC = 72 - 24 = 48 (cm2)
SABK = 48 : 2 = 24 (cm2)
Đáp số: a, SABCD = 144 cm2; SACM = 24 cm2
b, SABK = 24 cm2
BN
30 tháng 12 2017
Bạn tự vẽ hình nhé.
a) Xét tam giác AMB và tam giác DMC có: MB = MC (gt) ; góc AMB = góc DMC (2 góc đối đỉnh) ; AM = MD (gt)
=> tam giác AMB = tam giác DMC (c.g.c) (đpcm)
b) Vì AH vuông góc BC tại H (gt) (*) nên góc AHM = góc EHM = 90o (định nghĩa).
Xét tam giác HMA và tam giác HME có: chung HM ; góc AHM = góc EHM (cmt) ; HA = HE (gt)
=> tam giác HMA = tam giác HME (c.g.c) (1)
=> MA = ME (2 cạnh tương ứng) mà MA = MD (gt) nên ME = MD.
c) Vì ME = MD nên tam giác MDE cân tại M. => góc MED = góc MDE (t/c) (2)
Từ (1) => góc MAH = góc MEH (3)
Từ (2) và (3) => góc DEA = góc DAE + góc ADE => góc DEA = 90o
=> DE vuông góc AH. (**)
Từ (*) và (**) => DE // BC
