.Con lắc lò xo đặt nằm ngang có độ cứng k= 200 N/m, một đầu cố định, đầu kia gắn vật nhỏ nặng m = 100 g. Kéo vật m ra khỏi vị trí cân bằng 4 cm rồi thả nhẹ tay cho vật dao động. Bỏ qua ma sát. a) Tính thế năng đàn hồi của lò xo tại vị trí thả nhẹ tay? b) Tính vận tốc quả cầu tại vị trí cân bằng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2022
Câu 19.
a)Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot100\cdot0,05^2=0,125J\)
b)Cơ năng vật tại vị trí cân bằng:
\(W'=\dfrac{1}{2}mv^2+\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot0,2\cdot v^2+\dfrac{1}{2}\cdot100\cdot0^2\)
\(=0,1v^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow0,125=\dfrac{1}{2}mv^2\Rightarrow v=\dfrac{\sqrt{5}}{2}\)m/s
6 tháng 3 2022
Câu 20.
a)Động năng: \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25J\)
Thế năng: \(W_t=mgz=0,1\cdot10\cdot10=10J\)
Cơ năng: \(W=W_đ+W_t=1,25+10=11,25J\)
b)Cơ năng tại nơi có độ cao cực đại: \(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow11,25=mgh_{max}\Rightarrow h_{max}=\dfrac{11,25}{0,1\cdot10}=11,25m\)
c)Lực cản: \(F_c=0,2P=0,2\cdot10\cdot0,1=0,2N\)
Cơ năng tại nơi đây:
\(W_2=\left(mg+F_c\right)\cdot h'_{max}=\left(0,1\cdot10+0,2\right)\cdot h'_{max}\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow0,125=\left(0,1\cdot10+0,2\right)\cdot h'_{max}\)
\(\Rightarrow h'_{max}=0,1m\)
VT
23 tháng 4 2019
T = 0,63s ⇒ ω = 10
Tại t = 0 vật ở biên dương nên phương trình dao động của vật là
x = 10cos10t (cm)
VT
1 tháng 8 2018
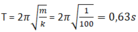
Tại t = 0 vật được kéo ra khỏi vị trí cân bằng cho lò xo dãn ra 10 cm rồi thả ra không vận tốc đầu nên biên độ A = 10 cm
VT
8 tháng 6 2019
Chọn đáp án D
? Lời giải:
+ Kéo vật đến vị trí lò xo giãn 5 cm rồi thả nhẹ, vật sẽ dao động quanh vị trí cân bằng với biên độ A = Δ l = 5 c m
+ Khi vật đi qua vị trí có li độ
lò xo tại điểm cách đầu cố định I một đoạn 0,75 chiều dài làm cho phần lò xo tham gia vào dao động mới của con lăc chỉ còn 0,25 → do đó thế năng của con lăc lúc sau chỉ còn lại là
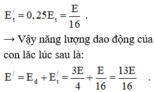
+ Mặc khác độ cứng của lò xo tỉ lệ nghịch với chiều dài nên con lăc lúc sau sẽ có độ cứng gấp 4 lần con lắc lúc đầu
VT
15 tháng 8 2018
Đáp án D
Kéo vật đến vị trí lò xo giãn 5 cm rồi thả nhẹ, vật sẽ dao động quanh vị trí cân bằng với biên độ 
Khi vật đi qua vị trí có li độ x =
A
2
= 2,5 cm, vật có độ năng
E
đ
=
3
E
4
và thế năng
T
1
=
E
4
→ việc giữ chặt lò xo tại điểm cách đầu cố định I một đoạn 0,75 chiều dài làm cho phần lò xo tham gia vào dao động mới của con lăc chỉ còn 0,25 → do đó thế năng của con lăc lúc sau chỉ còn lại là 
.
→ Vậy năng lượng dao động của con lăc lúc sau là: 
.
Mặc khác độ cứng của lò xo tỉ lệ nghịch với chiều dài nên con lăc lúc sau sẽ có độ cứng gấp 4 lần con lắc lúc đầu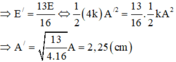 
VT
25 tháng 9 2019
Chọn đáp án D
? Lời giải:
+ Kéo vật đến vị trí lò xo giãn 5 cm rồi thả nhẹ, vật sẽ dao động quanh vị trí cân bằng với biên độ A = Δ l = 5 c m
+ Khi vật đi qua vị trí có li độ x = A 2 = 2,5 cm, vật có độ năng Eđ = 3 E 4 và thế năng T t = E 4 → việc giữ chặt
lò xo tại điểm cách đầu cố định I một đoạn 0,75 chiều dài làm cho phần lò xo tham gia vào dao động mới của con lăc chỉ còn 0,25 → do đó thế năng của con lăc lúc sau chỉ còn lại là E t / = 0 , 25 E t = E 16 .
→ Vậy năng lượng dao động của con lăc lúc sau là: E / = E d + E t / = 3 E 4 + E 16 = 13 E 16 .
+ Mặc khác độ cứng của lò xo tỉ lệ nghịch với chiều dài nên con lăc lúc sau sẽ có độ cứng gấp 4 lần con lắc lúc đầu
⇒ E / = 13 E 16 ⇔ 1 2 4 k A / 2 = 13 16 . 1 2 k A 2 ⇒ A / = 13 4.16 A = 2 , 25 c m
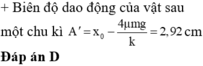
a)Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\left(\Delta x\right)^2=\dfrac{1}{2}\cdot200\cdot0,04^2=0,16J\)
b)Cơ năng tại vị trí cân bằng của quả cầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot v^2\)
Bảo toàn cơ năng: \(W_{đh}=W\)
\(\Rightarrow0,16=\dfrac{1}{2}\cdot0,1\cdot v^2\Rightarrow v=\dfrac{4\sqrt{5}}{5}\)m/s
E cảm ơn C Giang nhiều nha.😊