Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì ΔBAC vuông tại B
nên AB<AC
góc ACB<90 độ
=>góc ACD>90 độ
=>AC<AD
góc ACD>90 độ
=>góc CDA<90 độ
=>góc ADE>90 độ
=>AD<AE
=>AB<AC<AD<AE
a: ΔAHB vuông tại H
=>AH<AB
b: Xét ΔKAD vuông tại K và ΔHBA vuông tại H có
AD=BA
góc KAD=góc HBA
=>ΔKAD=ΔHBA
=>KD=HB và AK=BH
a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE
a.
b. Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a)
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
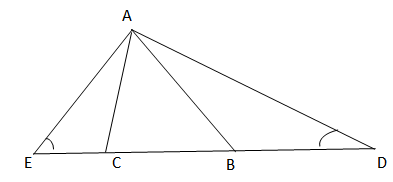
a) So sánh ˆADCADC^ và ˆAECAEC^
Ta có: AC < AB
=> ˆABC<ˆACBABC^<ACB^ (1)
Vì AC = EC => ∆AEC cân tại C
=> ˆAEC<ˆCAEAEC^<CAE^
Mà ˆACB=ˆAEC+ˆEACACB^=AEC^+EAC^ (góc ngoài tại C của ∆AEC)
=> ˆACB=2.ˆAECACB^=2.AEC^ (2)
Chứng minh tương tự : ˆABC=2ˆADCABC^=2ADC^ (3)
Từ (1), (2), (3) => 2ˆAEC=2ˆADC2AEC^=2ADC^ hay ˆAEC=ˆADCAEC^=ADC^
b) ∆AED có:
ˆAED=ˆADEAED^=ADE^ (chứng minh trên) => AD = AE
