Cho tam giác ABC vuông tại A AB bằng 8 cm AC bằng 60 cm Trên cạnh BC lấy điểm E sao cho be = ba
Tính độ dài cạnh BC
chứng minh BD là tia phân giác của góc B
Tính góc B bằng 60 độ tam giác ABC là tam giác gì Vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2022
a: BC=10cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó:ΔBAD=ΔBED
Suy ra: \(\widehat{ABD}=\widehat{EBD}\)
hay BD là tia phân giác của góc ABC
12 tháng 5 2019
C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
12 tháng 5 2019
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm
9 tháng 4 2022
a, BA = BD (gt)
=> Δ ABD cân tại B (đn)
góc ABC = 60 (gt)
=> Δ ABD đều (dấu hiệu)
b) Ta có\(\widehat{A}\)=90 độ và\(\widehat{B}\)=60 độ =>\(\widehat{C}\)=30 độ (1)
Mà BI là phân giác của \(\widehat{B}\)=> \(\widehat{IBC}\)=30 độ(2)
từ (1) và (2) => Δ IBC cân tại I
c) xét 2 tam giác BIA và BID có: \(\widehat{A}\)+\(\widehat{AIB}\)+\(\widehat{IBA}\)+\(\widehat{IBD}\)+\(\widehat{BDI}\)+\(\widehat{DIB}\)=360 độ
=> \(\widehat{AID}\)=120 độ
=> \(\widehat{DIC}\)=60 độ
Xét Δ BIA và Δ CID có:
DI=AI (Δ BIA=Δ BID)
\(\widehat{BIA}\)=\(\widehat{DIC}\)=60 độ
IB=IC(vìΔ IBC cân)
=>ΔBIA=Δ CID(c.g.c)
=> BA=CD mà BA=BD=> BD=DC
=> D là trung điểm của BC
d) vì AB=\(\dfrac{1}{2}\) BC nên BC=12 cm
Áp dụng định lí py-ta-go ta có:
BC2=AB2+AC2
=> AC2=BC2−AB2
=> AC2=144 - 36=108 cm
=> AC= \(\sqrt{108}\)(cm)
vậy BC=12 cm; AC= \(\sqrt{108}\)cm
18 tháng 3 2021
a)áp dụng định lý Py-Ta-Go cho ΔABC vuông tại A
ta có:
BC2=AB2+AC2
BC2=62+82
BC2=36+64=100
⇒BC=\(\sqrt{100}\)=10
vậy BC=10
AB và AC không bằng nhau nên không chứng minh được bạn ơi
còn ED và AC cũng không vuông góc nên không chứng minh được luôn
Xin bạn đừng ném đá
25 tháng 1 2019
a) Xét trong tam giác BIC từ định lí tổng 3 góc của một tam giác bằng 10 độ
=> \(\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}\)\(=180^o-\frac{1}{2}\widehat{ABC}-\frac{1}{2}\widehat{ACB}\)( tính chất phân giác)
\(=180^o-\frac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)
Mà xét trong tam giác ABC cũng từ định lí tổng ba góc của một tam giác bằng 180 độ
=> \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BCA}=180^o-60^o=120^o\)
=> \(\widehat{BIC}=180^o-\frac{1}{2}.120^o=120^o\)
b) Xét tam giác BEI và tam giác BFI
Hai tam giác này bằng nhau theo trường hợp góc cạnh góc (tự chứng minh)
=> \(\widehat{EIB}=\widehat{FIB}\)
Mà \(\widehat{EIB}=\widehat{DIC}=180^o-\widehat{BIC}=60^o\)
=> \(\widehat{BIF}=60^o\Rightarrow\widehat{CIF}=\widehat{BIC}-\widehat{BIF}=120^o-60^o=60^o\)
=> \(\widehat{CID}=\widehat{CIF}\)
Xét Tam giác IDC và tam giác IFC có:
IC chung
\(\widehat{CID}=\widehat{CIF}\)
\(\widehat{FIC}=\widehat{DIC}\)
=> \(\Delta CID=\Delta CIF\)(g-c-g)
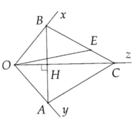
Điểm D ở đâu vậy bạn?