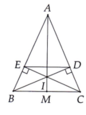
Cho tam giác ABC cân tại B ( góc B = 90° ) Kẻ AD vuông góc với BC, CE vuông góc vs AB ( D thuộc cạnh BC , E thuộc cạch AB ) a) Chứng minh ∆ BAD = ∆ BCE b) Gọi F là giao điểm của AD và CE. chứng minh BF là tia phân giác của góc ABC c) chứng minh FA > AC/2
Giúp mình vs


a: Xét ΔBAD vuông tại D và ΔBCE vuông tại E có
BA=BC
\(\widehat{ABD}\) chung
Do đó: ΔBAD=ΔBCE
b: Xét ΔBEF vuông tại E và ΔBDF vuông tại D có
BF chung
BE=BD
Do đó:ΔBEF=ΔBDF
Suy ra: \(\widehat{EBF}=\widehat{DBF}\)
hay BF là tia phân giác của góc ABC