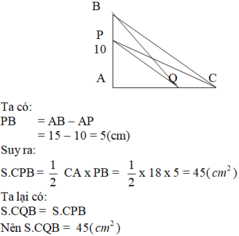
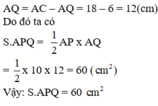Cho tam giác ABC có góc A vuông, có cạnh AB bằng 18cm; cạnh AC là 24cm. Điểm M nằm trên cạnh AC. Từ M kẻ đường thẳng song song với cạnh AB cắt cạnh BC tại N. Đoạn MN dài 12cm. Tính đoạn diện tích của tam giác AMN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2022
chấp hai tay xin mọi người
lướt qua thì làm hộ
ko thì đừng spam
cái gì ko liên quan đến đáp án sẽ báo cáo
và nhớ chình bày đầy đủ
DT
2 tháng 8 2016
\(\Delta ABH\)vuông ,ta có:
\(\tan B=\frac{AH}{BH}\Rightarrow AH=BH.\tan B=12.\tan60^o\approx16,517cm\)
\(\cos B=\frac{BH}{AB}\Rightarrow AB=\frac{BH}{\cos B}=\frac{12}{\cos12^o}\approx12,216cm\)
\(\tan C=\frac{AH}{HC}=\frac{16,517}{18}\approx0,918\Rightarrow C\approx26^o\)
\(\cos C=\frac{HC}{AC}\Rightarrow AC=\frac{HC}{\cos C}=\frac{18}{\cos26^o}\approx19,613cm\)
Vậy \(AH\approx16,517cm\)
\(AB=12,216cm\)
\(AC=19,613cm\)
3 tháng 1 2022
Cạnh AC dài \(10:\dfrac{1}{3}=30\left(cm\right)\)
Diện tích ABC là \(\dfrac{1}{2}\times30\times10=150\left(cm\right)\)
