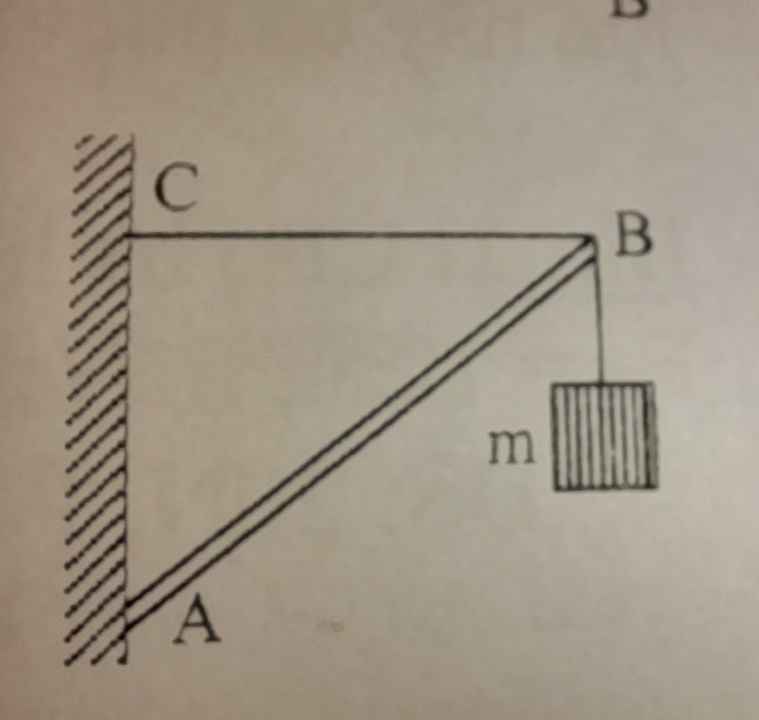
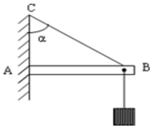
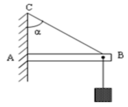
Một giá treo như hình vẽ gồm: Thanh AB = 1m tựa vào tường ở A, dây BC = 0,6m nằm ngang. Treo vào đầu B một vật nặng khối lượng m = độ lớn lực đàn hồi N xuất hiện trên thanh AB và sức căng của dây BC khi giá treo cân bằng. Lấy g = 10m/s và bỏ qua khối lượng thanh AB, các dây nối.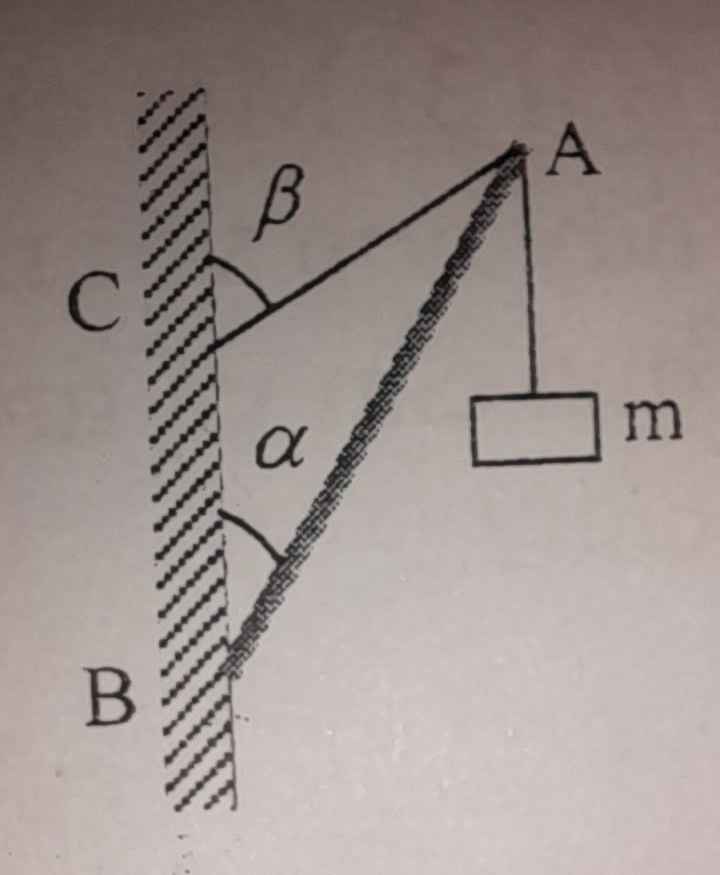
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

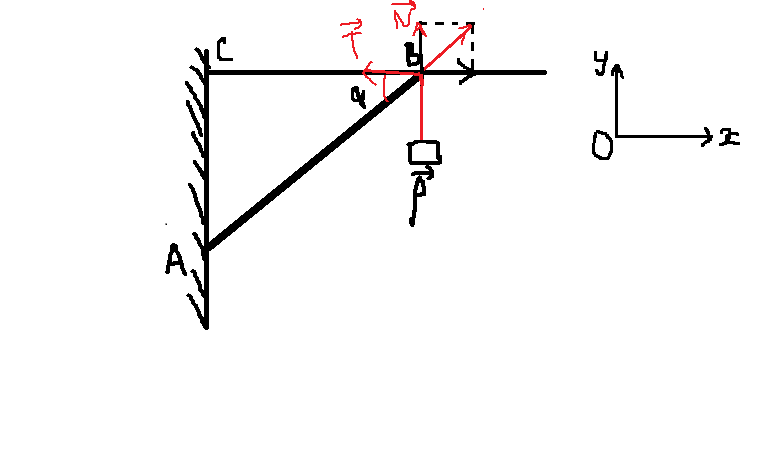
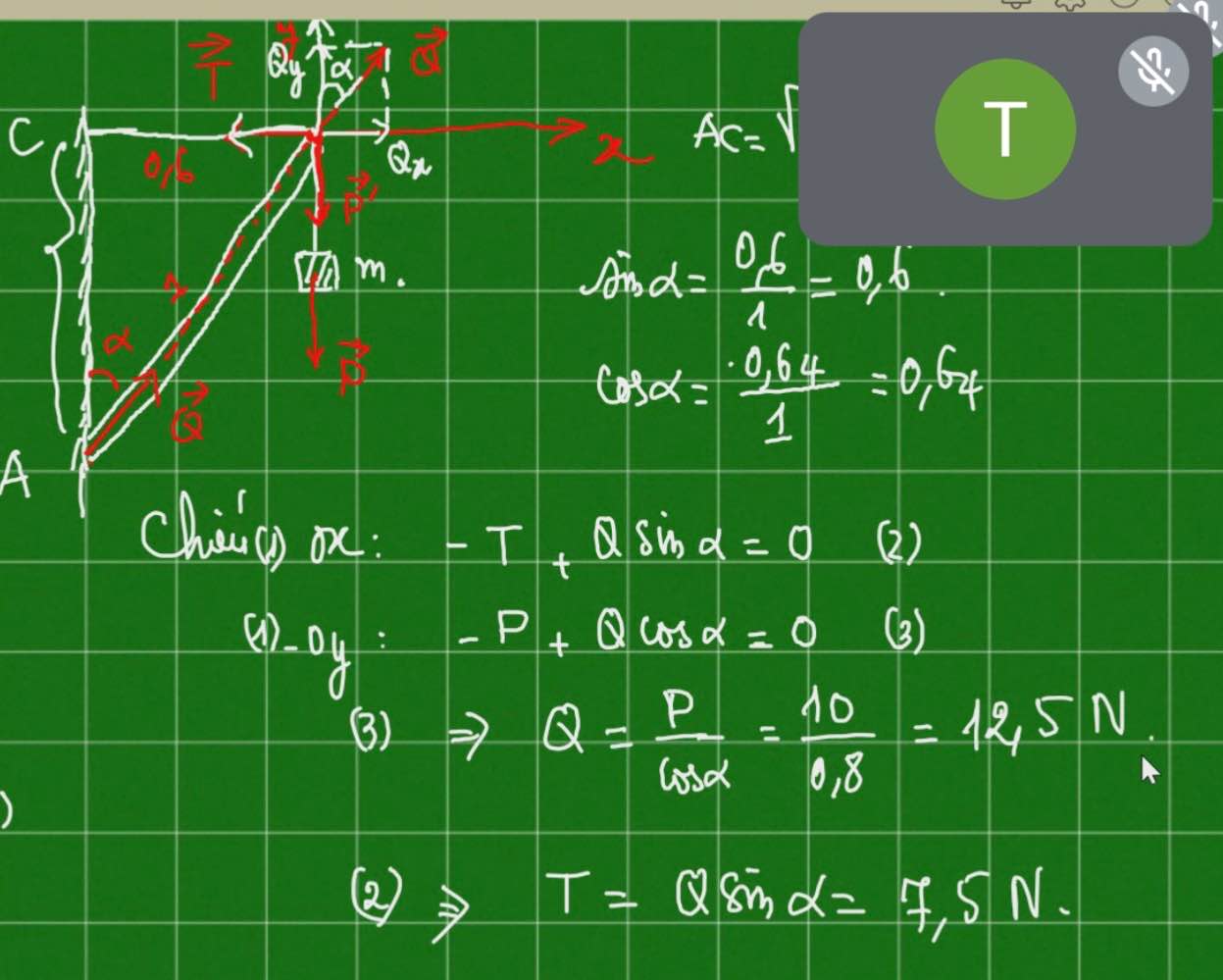
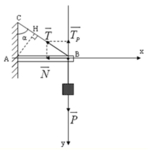
Các lực tác dụng lên thanh AB.
+Trọng lực \(\overrightarrow{P}\) hướng xuống.
+Lực căng dây \(\overrightarrow{T}\).
+Phản lực \(\overrightarrow{N}\).
Tổng hợp lực: \(\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{N}=\overrightarrow{0}\) \(\left(1\right)\)
Chiếu (1) lên trục Oxy ta đc:
Ox: \(Ncosa-T=0\)\(\Rightarrow T=Ncosa\)
Oy: \(Nsina-P=0\)\(\Rightarrow N=\dfrac{P}{sina}\)
\(cosa=\dfrac{BC}{AB}=\dfrac{0,6}{1}=0,6\)
\(sina=\sqrt{1-cos^2a}=\sqrt{1-0,6^2}=0,8\)
\(\Rightarrow N=\dfrac{P}{sina}=\dfrac{10m}{sina}=\dfrac{10\cdot1}{0,8}=12,5N\)
\(T=Ncosa=12,5\cdot0,6=7,5N\)

Chọn A.
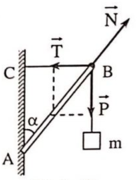
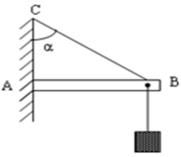
Các lực tác dụng lên thanh AB (tại B) như hình vẽ.
Điều kiện cân bằng: P ⇀ + N ⇀ + T ⇀ = 0
Từ hệ thức lượng trong tam giác vuông thu được:
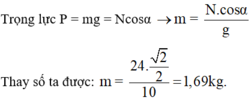
Vì α = 45° nên lực căng dây T = P = mg = 16,9N

Chọn A.
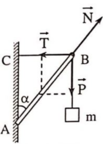
Các lực tác dụng lên thanh AB (tại B) như hình vẽ.
Điều kiện cân bằng:
P → + N → + T → = 0
Từ hệ thức lượng trong tam giác vuông thu được:
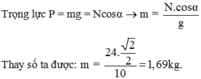
Vì α = 45° nên lực căng dây T = P = mg = 16,9N
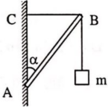
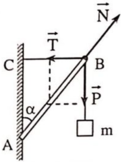

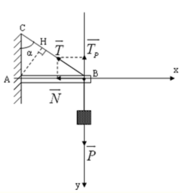
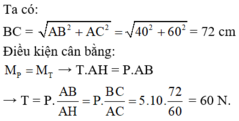
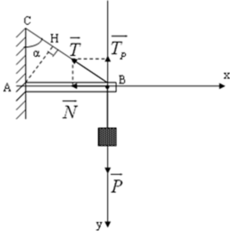
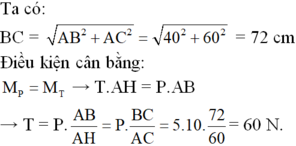
Các lực tác dụng lên thanh AB.
+Trọng lực \(\overrightarrow{P}\) hướng xuống.
+Lực căng dây \(\overrightarrow{T}\).
+Phản lực \(\overrightarrow{N}\).
Tổng hợp lực: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{T}=\overrightarrow{0}\left(1\right)\)
Chiếu (1) lên trục \(Oxy\) ta đc:
\(Ox:N\cdot cos\alpha-T=0\Rightarrow T=N\cdot cos\alpha\)
\(Oy:N\cdot sin\alpha-P=0\Rightarrow P=N\cdot sin\alpha\)
\(cos\alpha=\dfrac{BC}{AB}=\dfrac{0,6}{1}=0,6\)
\(\Rightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-0,6^2}=0,8\)
\(\Rightarrow N=\dfrac{P}{sin\alpha}=\dfrac{10m}{sin\alpha}=\dfrac{10\cdot1}{0,8}=12,5N\)
Lực căng dây:
\(T=N\cdot cos\alpha=12,5\cdot0,6=7,5N\)