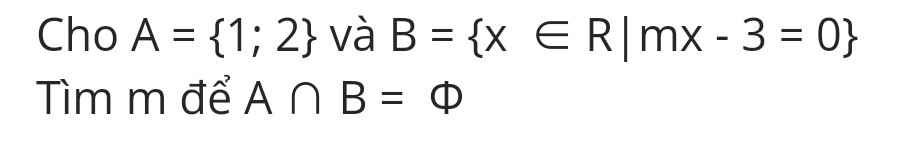(m-3)cos^2x -2(m-1)cosx +m+1=0. Gảii giúp mình trường hợp m khác 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 10 2020
3.
Theo điều kiện của pt lượng giác bậc nhất:
\(m^2+\left(3m+1\right)^2\ge\left(1-2m\right)^2\)
\(\Leftrightarrow10m^2+6m+1\ge4m^2-4m+1\)
\(\Leftrightarrow3m^2+5m\ge0\Rightarrow\left[{}\begin{matrix}m\ge0\\m\le-\frac{5}{3}\end{matrix}\right.\)
4.
\(\Leftrightarrow1-sin^2x-\left(m^2-3\right)sinx+2m^2-3=0\)
\(\Leftrightarrow-sin^2x-m^2sinx+2m^2+3sinx-2=0\)
\(\Leftrightarrow\left(-sin^2x+3sinx-2\right)+m^2\left(2-sinx\right)=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2-sinx\right)+m^2\left(2-sinx\right)=0\)
\(\Leftrightarrow\left(2-sinx\right)\left(sinx-1+m^2\right)=0\)
\(\Leftrightarrow sinx=1-m^2\)
\(\Rightarrow-1\le1-m^2\le1\)
\(\Rightarrow m^2\le2\Rightarrow-\sqrt{2}\le m\le\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 10 2020
1.
Bạn xem lại đề, \(sin^2x\left(\frac{x}{2}-\frac{\pi}{4}\right)\) là sao nhỉ?Có cả x trong lẫn ngoài ngoặc?
2.
ĐKXĐ: \(sinx\ne0\)
\(\left(2sinx-cosx\right)\left(1+cosx\right)=sin^2x\)
\(\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)=1-cos^2x\)
\(\Leftrightarrow\left(2sinx-cosx\right)\left(1+cosx\right)-\left(1+cosx\right)\left(1-cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\sinx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2021
Lý thuyết đồ thị:
Phương trình \(f\left(x\right)=m\) có nghiệm khi và chỉ khi \(f\left(x\right)_{min}\le m\le f\left(x\right)_{max}\)
Hoặc sử dụng điều kiện có nghiệm của pt lương giác bậc nhất (tùy bạn)
a.
\(\dfrac{\sqrt{3}}{2}\left(1-cos2x\right)+\dfrac{1}{2}sin2x=m\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x+\dfrac{\sqrt{3}}{2}=m\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{2}=m\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi:
\(-1+\dfrac{\sqrt{3}}{2}\le m\le1+\dfrac{\sqrt{3}}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2021
b.
\(\Leftrightarrow\dfrac{3}{2}\left(1-cos2x\right)-sin2x+m=0\)
\(\Leftrightarrow sin2x+\dfrac{3}{2}cos2x-\dfrac{3}{2}=m\)
\(\Leftrightarrow\dfrac{\sqrt{13}}{2}\left(\dfrac{2}{\sqrt{13}}sin2x+\dfrac{3}{\sqrt{13}}cos2x\right)-\dfrac{3}{2}=m\)
Đặt \(\dfrac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\dfrac{\sqrt{13}}{2}sin\left(2x+a\right)-\dfrac{3}{2}=m\)
Phương trình có nghiệm khi và chỉ khi:
\(\dfrac{-\sqrt{13}-3}{2}\le m\le\dfrac{\sqrt{13}-3}{2}\)
LL
9 tháng 7 2021
a) \(\sqrt{3}\left(\dfrac{1+cos2x}{2}\right)+\dfrac{1}{2}sin2x=m\) ↔ \(\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x=m-\dfrac{\sqrt{3}}{2}\)
→\(\sqrt{3}cos2x+sin2x=2m-\sqrt{3}\) ↔ \(2cos\left(\dfrac{\pi}{6}-2x\right)=2m-\sqrt{3}\)
→\(cos\left(\dfrac{\pi}{6}-2x\right)=m-\dfrac{\sqrt{3}}{2}\)
Pt có nghiệm khi và chỉ khi \(-1\le m-\dfrac{\sqrt{3}}{2}\le1\)
b) \(\left(3+m\right)sin^2x-2sinx.cosx+mcos^2x=0\)
cosx=0→ sinx=0=> vô lý
→ sinx#0 chia cả 2 vế của pt cho cos2x ta đc:
\(\left(3+m\right)tan^2x-2tanx+m=0\)
pt có nghiệm ⇔ △' ≥0
Tự giải phần sau
c) \(\left(1-m\right)sin^2x+2\left(m-1\right)sinx.cosx-\left(2m+1\right)cos^2x=0\)
⇔cosx=0→sinx=0→ vô lý
⇒ cosx#0 chia cả 2 vế pt cho cos2x
\(\left(1-m\right)tan^2x+2\left(m-1\right)tanx-\left(2m+1\right)=0\)
pt có nghiệm khi và chỉ khi △' ≥ 0
Tự giải
LP
0
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2019
a/ \(cos\left(3-2x\right)=-cosx=cos\left(\pi-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3-2x=\pi-x+k2\pi\\3-2x=x-\pi+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=3-\pi+k2\pi\\x=1+\frac{\pi}{3}+\frac{k2\pi}{3}\end{matrix}\right.\)
b/ \(cos\left(3-2x\right)=sinx=cos\left(\frac{\pi}{2}-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}3-2x=\frac{\pi}{2}-x+k2\pi\\3-2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=3-\frac{\pi}{2}+k2\pi\\x=1+\frac{\pi}{6}+\frac{k2\pi}{3}\end{matrix}\right.\)
c/ Tương tự câu trên \(cos\left(3+2x\right)=-sinx=cos\left(\frac{\pi}{2}+x\right)\Rightarrow...\)
d/ \(sin4x-\sqrt{3}sin2x=0\)
\(\Leftrightarrow2sin2x.cos2x-\sqrt{3}sin2x=0\)
\(\Leftrightarrow sin2x\left(2cos2x-\sqrt{3}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=\frac{\sqrt{3}}{2}\end{matrix}\right.\) \(\Rightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 8 2021
Trường hợp còn lại là \(m=0\Rightarrow mx-3=0\) vô nghiệm nên \(B=\varnothing\Rightarrow A\cap B=\varnothing\)
