Cho tam giác ABC vuông tại A, BK là tia phân giác của góc ABC (K thuộc AC). Lấy điểm I thuộc BC sao cho BI = BA. Chứng minh: \(KI \bot BC\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có gì khong hiểu hỏi lại cj nhé:
a, b ,c lần lượt từ trên xuống.

Bạn tự vẽ hình.
a, Sử dụng định lí pitago tính được \(BC=5cm\)
b, Dễ dàng chứng minh \(\Delta ABK=\Delta IBK\left(c.g.c\right)\)
=> \(\widehat{BIK}=\widehat{BAK}=90^o\)
=> \(KI\perp BC\)
c, Ta có: \(\hept{\begin{cases}AH\perp BC\\KI\perp BC\end{cases}}\)
=> AH // KI
=> \(\widehat{HAI}=\widehat{KIA}\) (1)
Mà AK = KI (do \(\Delta ABK=\Delta IBK\))
=> \(\Delta AKI\) cân tại K
=> \(\widehat{KAI}=\widehat{KIA}\) (2)
Từ (1) và (2) => \(\widehat{HAI}=\widehat{KAI}\)
=> AI là tia phân giác \(\widehat{HAC}\)
d, \(\Delta AEK\) có AI là phân giác => \(\Delta AEK\) cân tại A

a: Xét ΔABK và ΔIBK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔABK=ΔIBK
Suy ra: \(\widehat{BAK}=\widehat{BIK}=90^0\)
hay KI⊥BC
b: Ta có: \(\widehat{HAI}+\widehat{BIA}=90^0\)
\(\widehat{CAI}+\widehat{BAI}=90^0\)
mà \(\widehat{BIA}=\widehat{BAI}\)
nên \(\widehat{HAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc HAC

a: Xét ΔABD và ΔIBD có
BA=BI
\(\widehat{ABD}=\widehat{IBD}\)
BD chung
Do đó: ΔABD=ΔIBD

bn tham khảo tại đây;
https://olm.vn/hoi-dap/detail/256733768368.html

a.
Xét \(\Delta BAD\) và \(\Delta BKD\) có:
\(\left\{{}\begin{matrix}BA=BK\left(gt\right)\\\widehat{ABD}=\widehat{KBD}\left(gt\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BAD=\Delta BKD\left(c.g.c\right)\)
\(\Rightarrow AD=DK\)
b.
Cũng do \(\Delta BAD=\Delta BKD\Rightarrow\widehat{BKD}=\widehat{BAD}\)
Mà \(\widehat{BAD}=90^0\left(gt\right)\Rightarrow\widehat{BKD}=90^0\)
\(\Rightarrow DK\perp BC\)
\(\Rightarrow\widehat{ABK}=\widehat{CDK}\) (cùng phụ \(\widehat{ACB}\))
c.
Xét hai tam giác ADE và KDC có:
\(\left\{{}\begin{matrix}AD=DK\left(cmt\right)\\\widehat{ADE}=\widehat{KDC}\left(\text{đối đỉnh}\right)\\DE=DC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ADE=\Delta KDC\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAE}=\widehat{DKC}=90^0\)
\(\Rightarrow\widehat{BAE}=\widehat{BAC}+\widehat{DAE}=90^0+90^0=180^0\)
\(\Rightarrow B,A,E\) thẳng hàng
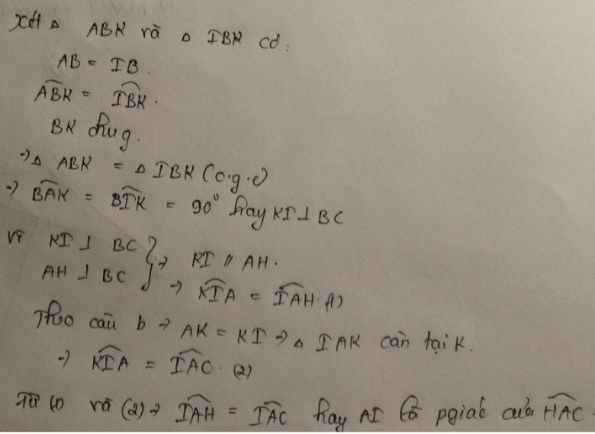
Hình bạn tự vẽ :
Xét \(\Delta ABK\)và \(\Delta IBK\)có :
\(BI=BA\left(gt\right)\)
\(\widehat{ABK}=\widehat{IBK}\left(gt\right)\)
\(BK\)chung
= > \(\Delta ABK=\Delta IBK\left(c.g.c\right)\)
= > \(\widehat{A}=\widehat{I}=90^0\)
hay \(KI\perp BC\)