gọi x1,x2 (x1>x2) là hai nghiệm của phương trình (3x-5)(8+x)-8x(5-3x)=0 giá trị của biểu thức x1-x2 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 4 2019
Phương trình ⇔ 4 x − 17 ≥ 0 x 2 − 4 x − 5 = 4 x − 17 2
⇔ x ≥ 17 4 x 2 − 5 x − 5 2 = 4 x − 17 2
⇔ x ≥ 17 4 ( x 2 − 8 x + 12 ) ( x 2 − 22 ) = 0 ⇔ x ≥ 17 4 x 2 − 8 x + 12 = 0 x 2 − 22 = 0
⇔ x ≥ 17 4 x = 2 ∨ x = 6 x = ± 22 ⇔ x = 6 x = 22 ⇒ P = 22 2 + 6 = 28
Đáp án cần chọn là: C
3 tháng 4 2023
Δ=(2m-2)^2-4(2m-5)
=4m^2-8m+4-8m+20
=4m^2-16m+24
=4m^2-16m+16+8=(2m-4)^2+8>=8>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(B=\dfrac{x_1^2}{x^2_2}+\dfrac{x_2^2}{x_1^2}\)
\(=\dfrac{x_1^4+x_2^4}{\left(x_1\cdot x_2\right)^2}=\dfrac{\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2}{\left(x_1\cdot x_2\right)^2}\)
\(=\dfrac{\left[\left(2m-2\right)^2-2\left(2m-5\right)\right]^2-2\left(2m-5\right)^2}{\left(2m-5\right)^2}\)
\(=\dfrac{\left(4m^2-8m+4-4m+10\right)^2}{\left(2m-5\right)^2}-2\)
\(=\left(\dfrac{4m^2-12m+14}{2m-5}\right)^2-2\)
\(=\left(\dfrac{4m^2-10m-2m+5+9}{2m-5}\right)^2-2\)
\(=\left(2m-1+\dfrac{9}{2m-5}\right)^2-2\)
Để B nguyên thì \(2m-5\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(m\in\left\{3;2;4;1;7\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
\(\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1^2+x_2^2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(-\dfrac{5}{3}\right)^2-2.\left(-2\right)-\left(-\dfrac{5}{3}\right)}{-2-\left(-\dfrac{5}{3}\right)+1}=...\)
2
13 tháng 1 2023
`1)` Ptr có: `\Delta=3^2-4.5.(-1)=29 > 0 =>`Ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-3/5),(x_1.x_2=c/a=-1/5):}`
Có: `A=(3x_1+2x_2)(3x_2+x_1)`
`A=9x_1x_2+3x_1 ^2+6x_2 ^2+2x_1x_2`
`A=8x_1x_2+3(x_1+x_2)^2=8.(-1/5)+3.(-3/5)^2=-13/25`
Vậy `A=-13/25`
____________________________________________________
`2)` Ptr có: `\Delta'=(-1)^2-7.(-3)=22 > 0=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2/7),(x_1.x_2=c/a=-3/7):}`
Có: `M=[7x_1 ^2-2x_1]/3+3/[7x_2 ^2-2x_2]`
`M=[(7x_1 ^2-2x_1)(7x_2 ^2-2x_2)+9]/[3(7x_2 ^2-2x_2)]`
`M=[49(x_1x_2)^2-14x_1 ^2 x_2-14x_1 x_2 ^2+4x_1x_2+9]/[3(7x_2 ^2-2x_2)]`
`M=[49.(-3/7)^2-14.(-3/7)(2/7)+4.(-3/7)+9]/[3x_2(7x_2-2)]`
`M=6/[x_2(7x_2-2)]` `(1)`
Có: `x_1+x_2=2/7=>x_1=2/7-x_2`
Thay vào `x_1.x_2=-3/7 =>(2/7-x_2)x_2=-3/7`
`<=>-x_2 ^2+2/7 x_2+3/7=0<=>x_2=[1+-\sqrt{22}]/7`
`@x_2=[1+\sqrt{22}]/7=>M=6/[[1+\sqrt{22}]/7(7 .[1+\sqrt{22}]/2-2)]=2`
`@x_2=[1-\sqrt{22}]/7=>M=6/[[1-\sqrt{22}]/7(7 .[1-\sqrt{22}]/2-2)]=2`
Vậy `M=2`
13 tháng 4 2020
Để pt: \(x^2-3x+m-2=0\) có hai nghiệm : \(x_1;x_2\) điều kiện là:
\(\Delta=9-4\left(m-2\right)\ge0\)
<=> \(m\le\frac{17}{4}\)( @@)
Áp dụng định lí viet ta có:
\(\hept{\begin{cases}x_1+x_2=3\\x_1.x_2=m-2\end{cases}}\)=> \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=9-4\left(m-2\right)=17-4m\ge0\)
=> \(x_1-x_2=\sqrt{17-4m}\)
Ta có:
\(x_1^3-x_2^3+9x_1x_2=\left(x_1-x_2\right)^3+3\left(x_1-x_2\right)x_1x_2+9x_1x_2\)
\(=\sqrt{\left(17-4m\right)^3}+3\sqrt{17-4m}\left(m-2\right)+9\left(m-2\right)\)
Theo bài ra ta có phương trình:
\(\sqrt{\left(17-4m\right)^3}+3\sqrt{17-4m}\left(m-2\right)+9\left(m-2\right)=81\)
<=> \(\left(\sqrt{17-4m}\right)^3-3^3+3\left(m-2\right)\left(\sqrt{17-4m}-3\right)=0\)
<=> \(\left(\sqrt{17-4m}-3\right)\left(17-4m+3\sqrt{17-4m}+9+3\left(m-2\right)\right)=0\)
<=> \(\left(\sqrt{17-4m}-3\right)\left(20-m+3\sqrt{17-4m}\right)=0\)
TH1: \(\sqrt{17-4m}-3=0\Leftrightarrow17-4m=9\Leftrightarrow m=2\left(tm@@\right)\)
TH2: \(20-m+3\sqrt{17-4m}=0\)
<=> \(3\sqrt{17-4m}=m-20\)=> \(m-20\ge0\)=> \(m\ge20\) vô lí với (@@)
Vậy m = 2.
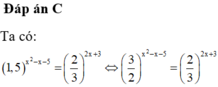
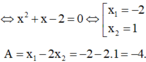
\(\left(3x-5\right)\left(x+8\right)+8x\left(3x-5\right)=0\)
=>(3x-5)(9x+8)=0
=>x=5/3 hoặc x=-9/8
\(x_1-x_2=\dfrac{5}{3}+\dfrac{9}{8}=\dfrac{40}{24}+\dfrac{27}{24}=\dfrac{67}{24}\)