Cho tam giac ABC có AB = 6, AC = 8. Đường trung tuyến BD vuông góc với trung tuyến CE. Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
2
10 tháng 11 2016
Goi G là giao điểm của 2 đường trung tuyến CE và BD ta có GD = 1/2 BG và EG = 1/2 CG [Vì theo tính chất của trung tuyến tại giao điểm G, của 3 đường ta có G chia đường trung tuyến ra làm 2 phần, phần này gấp đôi phần kia.]
Áp dụng định lý pythagore vào tam giác vuông BGE ta có:
BG^2 = EB^2 - EG^2 = 9 - EG^2 = 9 - (1/2. GC)^2 (1)
Áp dụng định lý pythagore vào tam giác vuông CGD ta có:
GC^2 = CD^2 - GD^2 = 16 - GD^2 = 16 - (1/2BG)^2 (2)
mặt khác BC^2 = BG^2 + GC^2. Do đó từ (1) và (2) ta có:
BC^2 = 9 -1/4 GC^2 + 16 - 1/4 BG^2 = 25 - 1/4(GC^2 + BG^2)
<=> BC^2 + 1/4(GC^2 + BG^2) = 25 <=> BC^2 + 1/4BC^2 = 25 <=> 5/4BC^2 = 25 <=>
BC^2 =25. 4/5 = BC^2 =20 <=> BC = căn 20 <=>
BC = 2.(căn 5) cm
12 tháng 8 2016
Gọi G là giao điểm của BD và CE. Ta có G là trọng tâm của △ABC
Đặt GD=x,GE=y. Khi đó GB=2x,GC=2y.
Áp dụng định lý Pitago cho các tam giác vuông BGE, CGD, ta có:
GE2+GB2=BE2⇒y2+4x2=9 (1)
GD2+GC2=CD2⇒x2+4y2=16 (2)
Từ (1) và (2) ta có: 5(x2+y2)=25
⇒x2+y2=5
Áp dụng định lý Pitago cho tam giác vuông BGC, ta có:
BC2=GB2+GC2=4x2+4y2=20
Vậy: BC = \(\sqrt[2]{5}\)
20 tháng 6 2015
goi G là gjao điểm của 2 trung tuyến BD ,CE.=>GB _|_ GC.khj đó điều pn cần làm là tính đk GB,GC==> phải tính đk BD,CE.
Kẻ đg cao BN ,CM của T.g ABC
Gọi V là gjao BN và CE
Gọi R là gjao CM và BD
khj đó,pn dễ dàng thấy B,M,G,N,C cùng nằm trên đg tròn đg kính BC.==>Góc GBV= GÓC GCD(1)
GÓC EBG= GÓC RCG (2) (Cák góc cùng chắn 1 dây cung)
==>tam gják BGV ~t.g CGD(g.g.g)
( góc BGV = góc CGD=90,và (1))
==>BV/CD=GV/GD=BG/CG=BD/CE
==>BV=CD.BD/CE (CD=AC/2=4 cm)
GV=GD.BD/CE =(BD/3).(BD/CE )
xét t.g vuông BGV( do G thuộk đg tròn đ.k BC) Ta có
BG^2+GV^2=BV^2
<==>BG ^2=BV^2-GV^2
Thay gjá trị ở trên có k.q
BG=[BD.Căn (16.9-BD^2)]/3CE
mà BG=2BD/3
==>BD^2+4CE ^2=16.9[3]
CMtương tự
xét 2 tam gják BGE ~ T.g CGR
==>4BD^2 + CE^2=81[4]
Giải hpt [3,4] pn tính đk
BD^2=12 , CE ^2=33
==>[BD^2+ CE ^2].[2/3]^2 = GB^2+GC^2 = BC^2 = 20 cm(do G là trọng tâm)
==> BC=2 Căn 5
Nguồn: cho tam giac abc co ab=6 ac=8, cac duong trung tuyen bd va ce vuong goc voi nhau. tinh bc??????? | Yahoo Hỏi & Đáp
27 tháng 6 2019
Các đường trung tuyến BD và CE vuông góc với nhau nên tam giác ABC vuông tại A
=> BC^2 = AB^2 + AC^2
=> BC^2 = 6^2 + 8^2
=> BC = 10 cm
KV
5 tháng 5 2023
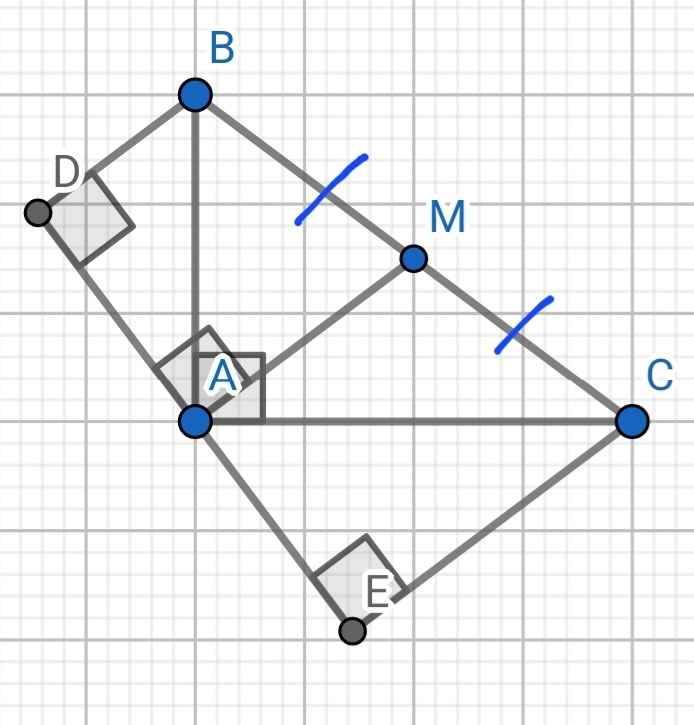
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)
Gọi H là giao điểm 2 đường trung tuyến BD và CE
=> H là trọng tâm trong tam giác ABC (vì là giao điểm 2 đường trung tuyến)
Ta có: BE = 3 , CD = 4
Áp dụng Py-ta -go ta được:
DH2 + CH2 = CD2 = 42 = 16 (1)
EH2 + BH2 = BE2 = 32 = 9 (2)
Cộng (1) và (2) vế theo vế ta được: DH2 + CH2 + EH2 + BH2 = 16 + 9 = 25
mà \(HD=\frac{1}{2}HB;HE=\frac{1}{2}HC\) nên : \(\frac{HB^2}{4}+HC^2+\frac{HC^2}{4}+HB^2=25\)
\(\Rightarrow\frac{5}{4}HB^2+\frac{5}{4}HC^2=25\Rightarrow HB^2+HC^2=20\)
Hay BC2 = 20 (vì HB2 + HC2 = BC2) => BC = \(2\sqrt{5}\)
Vậy \(BC=2\sqrt{5}\)