Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì ABCD là hình bình hành nên ME // DE và EN // AB.
+ ME // DC nên ΔAME ~ ΔADC, tỉ số đồng dạng A E A C = 1 3
+ Vì ABCD là hình bình hành nên góc B = D; AD = BC; AB = DC
=> ΔCBA ~ ΔADC
ΔCBA ~ ΔADC, tỉ số đồng dạng bằng 1
+ EN // AB nên ΔCNE ~ ΔADC, do đó ΔCNE ~ ΔADC, tỉ số đồng dạng C E A C = 2 3
Vậy cả (I), (II), (III) đều đúng.
Đáp án: C
Bài này là: Bài 27 trang 72 Toán 8 Tập 2 đúng không bạn
a) \(\Delta ABC\) có \(MN\) // \(BC\) \(\left(M\in AB;N\in AC\right)\Rightarrow\Delta AMN\sim\Delta ABC\) (định lí)
\(\Delta ABC\) có \(ML\) // \(AC\) \(\left(M\in AB;L\in BC\right)\Rightarrow\Delta MBL\sim\Delta ABC\) (định lí)
Vì \(\Delta AMN\sim\Delta ABC\) và \(\Delta MBL\sim\Delta ABC\)
\(\Rightarrow\Delta AMN\sim\Delta MBL\)
b) Xét \(\Delta AMN\sim\Delta ABC\) có:
\(\widehat{A}\) chung
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{C}\)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Tỉ số đồng dạng : \(k=\dfrac{AM}{AB}=\dfrac{1}{2}\left(AM=\dfrac{1}{2}MB\right)\)
Xét \(\Delta MBL\sim\Delta ABC\) có:
\(\widehat{B}\) chung
\(\widehat{BML}=\widehat{A};\widehat{MLK}=\widehat{C}\)
\(\dfrac{BM}{BA}=\dfrac{BL}{BC}=\dfrac{ML}{AC}\)
Tỉ số đồng dạng: \(k'=\dfrac{BM}{BA}=\dfrac{2}{3}\)
Xét \(\Delta AMN\sim\Delta MBL\) có:
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BML}\)
\(\dfrac{AM}{MB}=\dfrac{AN}{ML}=\dfrac{MN}{BL}\)
Tỉ số đồng dạng: \(k''=\dfrac{AM}{MB}=\dfrac{1}{2}\)
a: Xét ΔDAE và ΔBFE có
góc DAE=góc BFE
góc DEA=góc BEF
=>ΔDAE đồng dạng với ΔBFE
Xét ΔDEG và ΔBEA có
góc DEG=góc BEA
góc EDG=góc EBA
=>ΔDEG đồng dạng với ΔBEA
b: ΔDAE đồng dạng với ΔBFE
=>AE/FE=DE/BE=DA/BF
ΔDEG đồng dạng với ΔBEA
=>AE/EG=BE/DE
=>EG/AE=AE/FE
=>AE^2=EG*EF
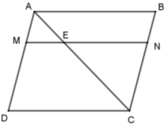
a, sửa tìm các tam giác đồng dạng nhé
Xét tam giác AME và tam giác ADC ta có : ME // DC
\(\frac{AM}{MD}=\frac{AE}{CE}\)( theo định lí Ta lét )
^A chung
Vậy tam giác AME ~ tam giác ADC ( c.c.c )
\(\Rightarrow\frac{ME}{DC}=\frac{AE}{AC}\)( tỉ số đồng dạng )
b, Xét tam giác ADC ta có : ME // DC
\(\Rightarrow\frac{AM}{AD}=\frac{AE}{AC}=\frac{ME}{DC}\)( theo hệ quả Ta lét )
Xét tam giác ACB ta có : EN // AB
\(\Rightarrow\frac{CE}{AC}=\frac{CN}{BC}=\frac{EN}{AB}\)( theo hệ quả Ta lét )
giả sử : E là trung điểm MN khi \(\frac{ME}{DC}=\frac{NE}{AB}\)
mà \(DC=AB\)( do ABCD là hình bình hành )
Suy ra : \(ME=NE\)hay E là trung điểm MN