Cho tứ giác ABCD có AB = CB, AD = AC = CD và góc A = 105 độ. Tính các góc của tứ giác ABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 5 2022
Bài 1:
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
b: Xét ΔBAC và ΔDAC có
AB=AD
AC chung
BC=DC
Do đó: ΔBAC=ΔDAC
Suy ra: \(\widehat{B}=\widehat{D}\)
=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)
BN
2
7 tháng 7 2015
mình vẽ hơi xấu
Xét hình tam giác ABD vá hình tam giác BCD
ab=bc(gt)
cd=ad(gt)
bd chung
do đó hình tam giác ABD=hình tam giác BCD (c.c.c)
=>A=C (hai góc tương ứng)
Mà A=105 độ nên C=105 độ
Tổng hai góc kề nhau =180 độ
nên A+B=180 độ
105 độ+B=180 độ
B=180 độ -105 độ
B=75 độ
Tổng 4 góc trong một tứ giác =360 độ
nên A+B+C+D=360 độ
105 độ+75 độ+105 độ+D=360 độ
D=360 độ -(105 độ+75 độ+105 độ)
D=75 độ
vậy A=C=105 độ
B=D=75 độ
23 tháng 6 2019
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
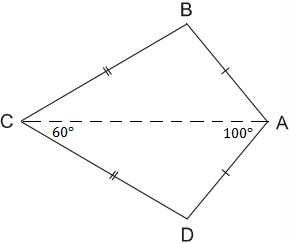
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000
