cho tam giác ABC có BC= 4cm , các trung tuyến BD , CE. Gọi M,Ntheo thứ tự là trung điểm của BE , CD. Gọi giao điểm của MN với BD , CE theo thứ tự là P và Q
a. tính độ dài MN
b.chứng minh rằng MP=PQ=QN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2017
Bạn tự vẽ hình nha
a) Vì D,E là trung điểm của AC và AB nên ED là đường trung bình của tam giác ABC.
Suy ra ED = \(\frac{BC}{2}\)= \(\frac{4}{2}\)= 2 (cm)
Tứ giác EDCB có ED // BC ( Vì ED là đường trung bình của tam giác ABC) nên EDCB là hình thang.
Vì M, N là trung điểm của EB và CD nên MN là đường trung bình của hình thang EDCB
suy ra MN = \(\frac{ED+BC}{2}\)= \(\frac{2+4}{2}\)=3 (cm).
Vậy MN =3 (cm)
b) Ta có MN// ED ( MN là đương tb củahình thang EDCB) nên MP//ED , QN//ED
Xét tg EBD có MP//ED (cmt)
MB =ME (gt)
Suy ra P là trung điểm của BD ,nên MP là đương tb của tg EBD nên MP= \(\frac{ED}{2}\)=\(\frac{2}{2}\)= 1(cm).
Chứng minh tương tự với tg ECD cũng có QN = 1(cm)
Ta có MN = MP + PQ +QN
3 = 1+PQ +1
QN =1 (cm)
Nên MP=PQ=QN.(đpcm)
Có nhìu chỗ thiếu xót mong mấy bạn thông cảm.
4 tháng 11 2021
Cho tam giác ABC, các đường trung tuyến BD, CE và BC = 8cm
a) Chứng minh rằng: Tứ giác BEDC là hình thang.
b) Gọi M, N theo thứ tự là trung điểm của BE, CD. Tính MN?
c) Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh rằng:
giúp cái
16 tháng 9 2020
a) Ta có : \(ED=\frac{BC}{2}=\frac{4}{2}=2\left(cm\right)\)
MN là đường trung bình của hình thang BEDC nên ta có :
\(MN=\frac{ED+BC}{2}=\frac{2+4}{2}=3\left(cm\right)\)
b) \(\Delta BED\)có BM = ME(vì M là trung điểm của BE) , mà MP // ED nên BP = PD . Do đó \(MP=\frac{ED}{2}=\frac{2}{2}=1\left(cm\right)\)
\(\Delta\)CED có NC = ND(vì N là trung điểm của CD) , mà NQ // ED nên CQ = CE . Do đó \(NQ=\frac{ED}{2}=\frac{2}{2}=1\left(cm\right)\)
Lại có : PQ = MN - MP - NQ = 3 - 1 - 1 = 1(cm)
Vậy MP = NQ = PQ = 1cm
T
1 tháng 8 2019
a) Đã có bài toán tương tự ở đây: Câu hỏi của zZz Cool Kid zZz (bạn thay tên các điểm cho phù hợp với bài này rồi làm theo hướng dẫn thôi)
b) ED là đường trung bình tam giác ABC nên ED// BC và \(ED=\frac{1}{2}BC=4\)(cm)
Áp dụng kết quả câu a): \(MN=\frac{BC-ED}{2}=\frac{8-4}{2}=\frac{4}{2}=2\) (cm)
c) Ta có MN = 2(cm) theo câu trên. (1)
MI là đường trung bình tam giác EBD nên \(MI=\frac{1}{2}ED=\frac{1}{2}.\frac{1}{2}BC=\frac{BC}{4}=\frac{8}{4}=2\) (2)
Tương tự \(NK=\frac{1}{2}ED=\frac{1}{4}BC=2\) (cm) (3)
Từ (1) và (2) và (3) suy ra \(MI=KN=MN\left(=2\right)\)
P/s: Câu c sai thì thôi nhé
CM
13 tháng 1 2017
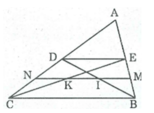
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
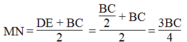
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC
