Cho ΔABC nhọn (AC<AB). Vẽ AM vuông góc (M ϵ BC)biết AC=15 cm, AM= 12cm, MB=9cm. Tính chu vi △ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(HC=\sqrt{15^2-12^2}=9\left(cm\right)\)
Xét ΔABC có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABC cân tại A
b: BH=CH=9cm

a) Xét tam giác ABC và tam giác HBA có :
∠ABC chung
∠BAC=∠BHA = 90
=> ΔABC ∼ ΔHBA (g.g)
b)Vì ΔABC ∼ ΔHBA
=> AB/BC = HB/BA (cặp cạnh tỉ lệ tương ứng)
=> AB^2 = BC.BH (tính chất tỉ lệ thức)
c) Áp dụng định lý Pytago vào tam giác ABC vuông tại A có :
BC^2= AB^2 +AC^2 = 9^2+12^2=225
=> BC=15
Vì AB^2= BC.BH
=> 9^2 = 15.BH =>BH = 5,4
Mà BH + CH = BC=15
=> CH = 9,6
Áp dụng định lý Pytago vào tam giác ABH vuông tại H có :
AB^2= AH^2+BH^2
=> AH^2 = AB^2 -BH^2 = 9^2 - 5,4^2 = 51,84
=> AH = 7,2
d) Vì BD là phân giác góc B
=> AD/DC = AB/BC (tính giác phân giác trong tam giác)
=> AD/AB = DC/BC = (AD+DC)/(AB+BC)= AC/(AB+BC)= 12/(9+15)=0,5 (tính chất tỉ lệ thức)
=> AD = 0,5 . AB = 0,5 . 9 =4,5
DC = 0,5 . BC = 0,5 . 15 =7,5
Lời giải:
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{BAC}=\widehat{BHA}=90^0$
$\widehat{B}$ chung
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
b.
Từ tam giác đồng dạng trên ta suy ra:
$\frac{AB}{HB}=\frac{BC}{BA}\Rightarrow AB^2=HB.BC$
c.
$BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15$ (cm)
$HB=\frac{AB^2}{BC}=\frac{9^2}{15}=5,4$ (cm)
$CH=BC-HB=15-5,4=9,6$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2$ (cm)
d.
Theo tính chất tia phân giác: $\frac{AD}{DC}=\frac{AB}{BC}=\frac{9}{15}=\frac{3}{5}$
$\Rightarrow \frac{AD}{AC}=\frac{3}{8}$
$\Rightarrow AD=\frac{3}{8}AC=4,5$ (cm)
$CD=AC-AD=12-4,5=7,5$ (cm)

Hướng dẫn:
∆
ABC ∼
∆
HAC nên 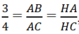
Suy ra HC = 4/3HA = 12. Chọn C.

mk chỉnh lại cái đề: tam giác ABC vuông tại A
BÀI LÀM
a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=9^2+12^2=225\)
\(\Leftrightarrow\)\(BC=\sqrt{225}=15\)
\(\Delta ABC\)có \(AD\)là phân giác \(\widehat{BAC}\)
\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\) (tính chất đường phân giác của tam giác)
\(\Rightarrow\)\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
hay \(\frac{BD}{3}=\frac{DC}{4}=\frac{BD+DC}{3+4}=\frac{15}{7}\)
\(\Rightarrow\)\(BD=\frac{15.3}{7}=\frac{45}{7}\)
\(DC=\frac{15.4}{7}=\frac{60}{7}\)
Áp dụng định lý pitago vào tam giác vuông AMB,có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AB=\sqrt{12^2+9^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông AMC, có:
\(AC^2=AM^2+CM^2\)
\(\Rightarrow CM=\sqrt{AC^2-AM^2}=\sqrt{15^2-12^2}=\sqrt{81}=9cm\)
\(C_{ABC}=AB+AC+BC=15+15+\left(9+9\right)=48cm\)
Áp dụng định lí Pytago ta có
\(AB^2=AM^2+MB^2\\ =\sqrt{12^2+9^2}=15\)
Chu vi tam giác ABC là
\(15+15+9+9=48\left(cm\right)\)