Cho tam giác ABC vuông tại A có AB=21cm , AC=28cm.Đường phân giác của góc A cắt BC tại D.Đường thẳng qua DE // AB(E thuộc AC)
a,Tính BD,DC,DE
b, Tính diện tích tam giác ABD và diện tích tam giác ACD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{9}=\dfrac{CD}{12}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{9}=\dfrac{CD}{12}=\dfrac{BD+CD}{9+12}=\dfrac{BC}{21}=\dfrac{15}{21}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{9}=\dfrac{5}{7}\\\dfrac{CD}{12}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{45}{7}cm\\CD=\dfrac{60}{7}cm\end{matrix}\right.\)
Vậy: \(BD=\dfrac{45}{7}cm;CD=\dfrac{60}{7}cm\)
CM
25 tháng 12 2019
Ta có: S A B C = 1/2.AB.AC = 1/2.21.28 = 294 ( c m 2 )
Vì △ ABC và △ ADB có chung đường cao kẻ từ đỉnh A nên:
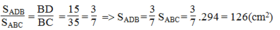
Vậy S A D C = S A B C - S A B D = 294 – 126 = 168( c m 2 )
1 tháng 3 2021
Bổ sung đề: AC=28cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+28^2=1225\)
hay BC=35(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{21}=\dfrac{DC}{28}\)
mà DB+DC=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{21}=\dfrac{DC}{28}=\dfrac{DB+DC}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{21}=\dfrac{5}{7}\\\dfrac{CD}{28}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=15\left(cm\right)\\CD=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC có
D∈BC(gt)
E∈AC(gt)
DE//AB(gt)
Do đó: \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)(Hệ quả Định lí Ta lét)
\(\Leftrightarrow\dfrac{DE}{21}=\dfrac{20}{35}\)
hay \(DE=\dfrac{21\cdot20}{35}=\dfrac{420}{35}=12\left(cm\right)\)
Vậy: CD=15cm; BD=20cm; DE=12cm
