Cho tam giác $ABC$ vuông tại $A$, nội tiếp trong đường tròn tâm $I$; bán kính $r$. Gọi $P$ là trung điểm của $AC$; $AH$ là đường cao của tam giác $ABC$.
a) Chứng minh tứ giác $APHI$ nội tiếp được trong đường tròn. Xác định tâm $K$ của đường tròn này.
b) Chứng minh hai đường tròn $(I)$ và $(K)$ tiếp xúc nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
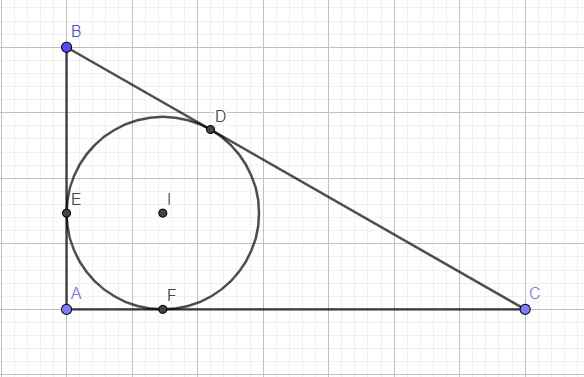
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)
TN
15 tháng 6 2016
a)\(\Delta AEC\)có góc ngoài là AEB=góc KAC+ góc ACE
Mà góc BAE = góc KAH; góc ACB = góc BAH => góc AEB = góc BAE
\(\Rightarrow\Delta ABE\)cân ở B và có BJ là phân giác
=>BJ vuông góc với AE
Tương tự có CJ vuông góc AD => AI vuông góc JK (I là trực tâm \(\Delta AJK\))
b)Dùng tính chất các phân giác ta có: góc BAI= góc \(\frac{BAC}{2}=\)\(\frac{\text{(góc B+góc C)}}{2}\)
=>Góc EAI=\(\frac{\text{(góc B+góc C)}}{2}\text{-góc EAI}\)\(\frac{\text{(góc B+góc C)}}{2}\text{- góc C}=\frac{\text{góc B}}{2}\)
Nhưng ta lại có góc EAI=JAI=EKJ (Cùng phụ góc AJK)
=>Góc EKJ= góc JBC(= góc B/2)
Lại có góc EKJ+góc JKC=180 độ (kề bù)
=>góc JBC+góc JKC=180 độ nên tứ giác BJKC nội típ
oke bạn