Tìm giá trị của k để các đường thẳng sau: \(y=\frac{6-x}{4}\); \(y=\frac{4x-5}{3}\) và y = kx + k + 1 cắt nhau tại một điểm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VK
0
2 tháng 4 2020
Gọi \(y=\frac{6-x}{4}\)và \(y=\frac{4x-5}{3}\)cắt nhau tại A
\(\Rightarrow\frac{6-x}{4}=\frac{4x-5}{3}\)
<=> 18-3x=16x-20
=> x=2 => y=1
=> A(2;1)
\(A\in y=kx+k+1\)nên \(1=k\cdot2+k+1\)
=> k=0
14 tháng 8 2021
a: Thay x=0 và y=0 vào \(\left(d\right)\), ta được:
k=0
30 tháng 8 2021
Bài 2:
Để hai đường thẳng này trùng nhau thì
\(\left\{{}\begin{matrix}k=5-k\\m-2=4-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2k=5\\2m=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=\dfrac{5}{2}\\m=3\end{matrix}\right.\)
CM
16 tháng 6 2019
Đường thẳng y = (k + 1)x + k song song với đường thẳng y = ( 3 +1)x+3 khi và chỉ khi:
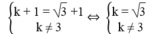
Vậy hàm số có dạng: y = ( 3 + 1)x + 3
NA
23 tháng 12 2018
a) (d) đi qua điểm (1;2)
<=> 2 = k + 1 + k
<=> 1 = 2k
<=> k = 0,5
Vậy k = 0,5 thì (d) đi qua (1;2)
b) Để (d) // đgth y = 2x + 3
\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)
Vậy k =1 thì (d) // đgth y = 2x +3
c) Gọi điểm cố định là (d) đi qua là (x0;y0)
Ta có y0 = ( k +1) x0 + k
<=> y0 = kx0 + x0+k
<=> y0 - x0 - k ( x0 + 1) = 0 \(\forall\)k
Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)
Điểm cố định (d) luôn đi qua là ( -1;-1)
CM
18 tháng 11 2019
Đường thẳng y = (k + 1)x + k có dạng là hàm số bậc nhất đi qua gốc tọa độ nên k = 0
Vậy hàm số có dạng: y = x
cho (6 - x) / 4 = (4x - 5 ) / 3
tìm ra x suy ra được y
thay x và y vào y = kx + k + 1 tìm ra k