Cho một số tự nhiên, nếu viết thêm một chữ số vào bên phải số đó ta được số mới hơn số đã cho 2004 đơn vị. Tìm số đã cho và chữ số viết thêm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 8 2019
Cách 1 : Khi viết thêm một chữ số nào đó vào bên phải một số tự nhiên đã cho ta được số mới bằng 10 lần số tự nhiên đó cộng thêm chính chữ số viết thêm. Gọi chữ số viết thêm là a, ta có sơ đồ
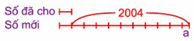
9 lần số đã cho là : 2004 - a.
Số đã cho là : (2004 - a) : 9.
Vì số đã cho là số tự nhiên nên 2004 - a phải chia hết cho 9, số 2004 chia 9 dư 6 nên a chia cho 9 phải dư 6, mà a là chữ số nên a = 6. Số tự nhiên đã cho là (2004 - 6) : 9 = 222.
Cách 2 : Gọi số tự nhiên đã cho là A chữ số viết thêm là x thì số mới là A x ¯ .
Ta có A x ¯ - A = 2004
A x 10 + x - A = 2004 (phân tích số)
A x 10 - A + x = 2004
A x (10 - 1) + x = 2004 (một số nhân với một tổng)
A x 9 + x = 2004
Vì A x 9 chia hết cho 9 ; 2004 chia 9 dư 6 nên x chia cho 9 phải dư 6. Vì x là chữ số nên x = 6. Ta có :
A x 9 + 6 = 2004
A x 9 = 2004 - 6
A x 9 = 1998
A = 1998 : 9
A = 222.
Vậy số tự nhiên đã cho là 222 ; chữ số viết thêm là 6.
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 8 2021
gọi số ban đầu là x, chữ số thêm vào là y
khi đó ta có số mới có giá trị là \(10\times x+y\)
ta có :\(10\times x+y-x=2004\)
hay \(9\times x+y=2004\text{ hay }9x=2004-y\)
nên \(11139-y\text{ chia hết cho 9}\) mà y là chữ số nên \(0\le y\le9\)
\(\Rightarrow y=6\)
vậy số thêm vào là 6
1 tháng 8 2016
số viết thêm là
2004 : (10-1) = 222 dư6
vậy số viết thêm là 6
1 tháng 8 2016
Gọi số cần tìm là N.
Nếu viết thêm một chữ số vào bên phải số đó thì ta được một số gấp số cũ 10 lần và N đơn vị.
Số N là:
2004 : ( 10 - 1 ) = 6
Vậy số đó là 6.
4 tháng 8 2015
ta có : 2013/(10-1)=223[dư 6]
vậy số đã cho là 223 . chữ số viết thêm là 6
7 tháng 3 2016
Ta có: 2004 : 9 = 222 (dư 6)
Vậy chữ số viết thêm là 6 và số tự nhiên ban đầu là 222
Số viết thêm là :
2004 : ( 10 - 1 ) = 222 ( dư 6 )
Vậy số viết thêm là 6
Số viết thêm là :
2004 : ( 10-1 ) = 222 dư 6
Vậy số viết thêm là 6