Nam lấy ra ngẫu nhiên một viên bi từ trong hộp có chứa 4 viên bi xanh, 3
viên bi đỏ, 3 viên bi vàng, 2 viên bi tím
a. Liệt kê tất cả các kết quả có thể xảy ra đối với màu của viên bi
b. Nêu 2 điều cần chú ý trong mô hình xác suất của trò chơi trên
c. Tính xác xuất lấy được viên bi màu tím.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Có 3 kết quả có thể xảy ra
b. Sự kiện đó không thể luôn xảy ra
c. Xác suất thực nghiệm lấy được bi màu xanh là: \(\dfrac{4}{4+3+3}=0,4=40\%\)
Có 3 kết quả có thể xảy ra đối với màu của viên bi đc lấy ra, đó là:
Sự kiện “Nam lấy được viên bi xanh” không luôn xảy ra.
Xác suất lấy được viên bi màu xanh là:

Đáp án D.
1. Tìm không gian mẫu.
Bạn Hà lấy ngẫu nhiên 2 viên bi có C 6 2 trường hợp.
Bạn Lâm lấy ngẫu nhiên 2 viên bi trong 4 viên còn lại có C 4 2 trường hợp.
Bạn Anh lấy 2 viên bi còn lại có 1 trường hợp.
Vậy n Ω = C 6 2 . C 4 2 = 90 .
2. Gọi A là biến cố “Hai viên bi bạn Anh lấy ra có cùng màu”.
Trường hợp 1: Hai viên bi bạn Anh lấy ra có cùng màu đỏ thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6 .
Trường hợp 2: Hai viên bi bạn Anh lấy ra có cùng màu xanh thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6
Trường hợp 3: Hai viên bi bạn Anh lấy ra có cùng màu vàng thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6 .
⇒ n A = 6.3 = 18 ⇒ P A = n A n Ω = 18 90 = 1 5

Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 14 viên bi.
Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố 6 viên bi được lấy ra có đủ cả ba màu . Để tìm số phần tử của biến cố A ta đi tìm số phần tử của biến cố ![]() tức là 6 viên bi lấy ra không có đủ ba màu như sau:
tức là 6 viên bi lấy ra không có đủ ba màu như sau:
● Trường hợp 1. Chọn 6 viên bi chỉ có một màu (chỉ chọn được màu vàng).
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Chọn 6 viên bi có đúng hai màu xanh và đỏ, có ![]() cách.
cách.
Chọn 6 viên bi có đúng hai màu đỏ và vàng, có ![]() cách.
cách.
Chọn 6 viên bi có đúng hai màu xanh và vàng, có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố ![]() .
.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 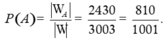
Chọn B.
