Phân tích đa thức x2 +x -6 thành nhân tử
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 10 2017
x2 – x – 6
= x2 + 2x – 3x – 6
(Tách –x = 2x – 3x)
= x(x + 2) – 3(x + 2)
(có x + 2 là nhân tử chung)
= (x – 3)(x + 2)
PT
1
CM
24 tháng 9 2019
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
a) x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
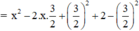
(Vì có x2 và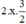 
nên ta thêm bớt 
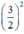để xuất hiện HĐT)
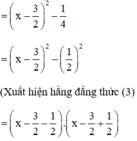
= (x – 2)(x – 1)
b) x2 + x - 6
= (x – 2)(x + 3).
c) x2 + 5x + 6
= (x + 2)(x + 3).
21 tháng 8 2021
\(\left(x^2+x+1\right)\left(x^2+x+5\right)-21=x^4+x^3+5x^2+x^3+x^2+5x+x^2+x+5-21=x^4+2x^3+7x^2+6x-16=\left(x-1\right)\left(x+2\right)\left(x^2+x+8\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
\(=\left(x^2+x+1\right)\left(x^2+x+1+4\right)-21\)
\(=\left(x^2+x+1\right)^2+4\left(x^2+x+1\right)-21\)
\(=\left(x^2+x+1\right)^2-3\left(x^2+x+1\right)+7\left(x^2+x+1\right)-21\)
\(=\left(x^2+x+1\right)\left(x^2+x-2\right)+7\left(x^2+x-2\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+8\right)\)
\(=\left(x-1\right)\left(x-2\right)\left(x^2+x+8\right)\)
16 tháng 11 2021
\(=3\left(x-1\right)+x\left(x-1\right)\)
\(=\left(x-1\right)\left(x+3\right)\)
GL
1 tháng 7 2023
\(\Leftrightarrow x^3-2x^2+x^2-2x+x-2\)
\(\Leftrightarrow x^2\left(x-2\right)+x\left(x-2\right)+\left(x-2\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)\)
PV
1
2 tháng 3 2022
-Đặt \(t=\left(x^2-x+1\right)\)
\(\left(x^2-x+1\right)^2-5x\left(x^2-x+1\right)+4x^2\)
\(=t^2-5xt+4x^2\)
\(=t^2-4xt-xt+4x^2\)
\(=t\left(t-4x\right)-x\left(t-4x\right)\)
\(=\left(t-4x\right)\left(t-x\right)\)
\(=\left(x^2-x+1-4x\right)\left(x^2-x+1-x\right)\)
\(=\left(x^2-5x+1\right)\left(x^2-2x +1\right)\)
\(=\left(x^2-5x+1\right)\left(x-1\right)^2\)
\(x^2+x-6=x^2-2x+3x-6=x\left(x-2\right)+3\left(x-2\right)=\left(x-2\right)\left(x+3\right)\)
x2 + x - 6
= x2 - 2x + 3x - 6
= x ( x - 2 ) + 3 ( x - 2 )
= ( x - 2 ) ( x + 3 )