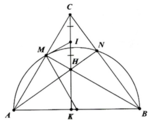
Cho nửa đường tròn $(O)$ đường kính \(AB=2R\) và điểm $C$ nằm trong nửa mặt phẳng chứa nửa đường tròn và nằm ngoài nửa đường tròn. $CA$ cắt nửa đường tròn ở $M$, $CB$ cắt nửa đường tròn ở $N$. Gọi $H$ là giao điểm của $AN$ và $BM$.
a) Chứng minh \(CH\perp AB\).
b) Gọi $I$ là trung điểm của $CH$. Chứng minh $MI$ là tiếp tuyến của nửa đường tròn $(O)$.
c) Giả sử $CH$ = $2R$. Tính số đo cung \(\stackrel\frown{MN}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
Xét ΔCAB có
AN,BM là các đường cao
AN cắt BM tại H
Do đó: H là trực tâm
=>CH vuông góc với AB
b: góc IMO=góc IMH+góc OMH
=90 độ-góc ACH+góc ABM
=90 độ
=>MI là tiếp tuyến của (O)

a, HS tự chứng minh
b, Gọi CH ∩ AB = K
Chứng minh được ∆MIC cân tại I
=> I C M ^ = I M C ^
Tương tự: O M A ^ = O A M ^
Chứng minh được I M O ^ = 90 0 => ĐPCM

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
=>ΔANB vuông tại N
Xét ΔCAB có
AN.BM là đường cao
AN cắt BM tại H
=>H là trực tâm
=>CH vuông góc AB
b:
Gọi giao của CH vơi AB là K
=>CH vuông góc AB tại K
góc OMI=góc OMH+góc IMH
=góc OBM+góc IHM
=góc OBM+góc BHK=90 độ
=>IM là tiếp tuyến của (O)

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB

a) Vì AD là tia phân giác của góc CAB⇒góc CAH= góc HAB
mà góc CAH là góc nội tiếp chắn cung CH
góc HAB là góc nội tiếp chắn cung HB
⇒ cung CH=cung HB
Ta có: góc HBC là góc nội tiếp chắn cung CH
góc HBD là góc tạo bởi tia tiếp tuyến và dây cung chắn cung HB
⇒ góc HBC = góc HBD
lại có: góc AHB chắn nửa (O)⇒góc AHB=90o⇒AH\(\perp\)HB
Xét ΔFBD có: BH là đường cao đồng thời là đường phân giác
⇒ΔFBD cân tại B⇒FB=DB
Và BH là đường trung tuyến ⇒FH=FD
b)Ta có: góc ACB là góc nội tiếp chắn nửa (O)
⇒ góc ACB= 90o
Xét ΔABM vuông tại B có BC là đường cao ứng với cạnh huyền AM
AC.AM=AB2 ( hệ thức lượng trong Δ vuông ) (1)
Xét ΔABD vuông tại B có BH là đường cao ứng với cạnh huyền AD
AH.HD=AB2 ( hệ thức lượng trong Δ vuông ) (2)
Từ(1) và(2)⇒AC.AM=AH.HD
a) vì góc CAH= góc HAB( AH là p/g của góc CAB)
=> cung CH= cung BH
Ta có : sđ góc CBH=1/2 sđ cung CH( góc nt chắn cung CH) => góc CBH=1/2 cung BH (1)
sđ góc HBM=1/2 sđ cung BH ( góc tạo bởi tia tiếp tuyến và dây cung chắn cung BH) (2)
Từ 1 và 2 => góc CBH= góc HBM => CH là p/g của góc FBD
xét △ BDF có: CH là p/g của góc FBD
Mà BH còn là đường trung trực của FD( góc ABH chắn nửa đường tròn)
=>△BDF cân tại B => FB=DB : HF=HD
b) xét △ABM vuông tại B có: AC.AM=AB bình( hệ thức lượng trong tam giác vuông) (3)
△ABD vuông tại B có: AH.AD=AB bình( hệ thức lượng trong tam giác vuông) (4)
từ 3 và 4 => AC.AM=AH.AD_đpcm

CH=2R =90
xét jfnfjdmemekekd