từ các chứ số 1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên có 5 chữ số, trong đó chữ số 3 có mặt đúng 3 lần, các chữ số còn lại có mặt không quá 1 lần. Trong các số tự nhiên nói trêntìm xác suất để số được chọn chia hết cho 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2021
Số chữ số tìm được là \(\dfrac{C^2_5\cdot5!}{3!}=200\)
Số số chia hết cho 3 là \(\dfrac{2\cdot5!}{3!}=40\)
\(\Rightarrow P=\dfrac{40}{200}=\dfrac{1}{5}\)
19 tháng 7 2018
ta có : vì chữ số 4 có mặc 3 lần nên \(\Rightarrow\) bài toán tương đương với việc tìm số lượng của số có 7 chữ số được tạo bởi các con số : \(0,1,2,3,4,4,4\)
bước 1: tìm số lượng tất cả các số được tạo bởi bao gồm trường hợp chữ số 0 ở đầu .
ta có : số cách sắp xếp vị trí cho 3 chữ số 4 là : \(C^3_7=35\)
số cách sắp xếp vị trí cho 4 chữa số \(0,1,2,3\) là : \(P^4_4=4!=24\)
\(\Rightarrow\) có \(35.24=840\) (số)
bước 2: tìm số lượng số có chữ số 0 ở đầu
ta có : số cách sắp xếp vị trí cho 3 chữ số 4 ở 6 vị trí còn lại là : \(C^3_6=20\)
số cách sắp xếp vị trí cho 3 chữa số \(1,2,3\) ở 3 vị trí còn lại là : \(P^3_3=3!=6\)
\(\Rightarrow\) có : \(20.6=120\) (số)
\(===\Rightarrow\) số lượng số cần tìm bằng : \(840-120=720\) (số)
25 tháng 10 2021
em hong thấy chữ với hình như cũng 0 đúng đề á :))
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 10 2021
TH1: chữ số 0 có mặt 2 lần:
Có \(\dfrac{7!}{2!.2!.3!}-\dfrac{6!}{2!.3!}=150\) số
TH2: số 1 có mặt 2 lần:
Có \(\dfrac{7!}{2!.2!.3!}=210\) số
TH3: số 0 và số 1 mỗi số có mặt 1 lần:
\(\dfrac{7!}{1!.1!.2!.3!}-\dfrac{6!}{1!.2!.3!}=360\) số
Tổng cộng: \(150+210+360=720\) số
1 tháng 4 2023
Gọi số cần tìm là \(\overline{abcdefgh}\)
TH1: h=0
Bỏ 2 ô mà có thể số 1 đứng cạnh nhau ta được 5 ô còn lại có trống để cho số 1 vào
=>Có \(C^3_5\left(cach\right)\)
Số cách chọn cho 4 ô trống còn lại là: \(A^4_8\left(cách\right)\)
=>Có \(C^3_5\cdot A^4_8\left(cách\right)\)
TH2: h<>0
=>h có 4 cách
Số cách chọn cho vị trí số 1 là \(C^3_5\left(cách\right)\)
=>SỐ cách chọn cho các vị trí còn lại là: \(A^4_8\left(cách\right)\)
Nếu số 0 đứng đầu thì trừ đi số ô nhét số 1 vào thì còn 4 ô và có \(C^3_4\) cách nhét số1
=>Số cách chọn cho 3 vị trí còn lại là \(A^3_7\left(cách\right)\)
=>Trường hợp này có \(4\cdot\left(A^4_8\cdot C^3_5-A^3_7\cdot C^3_4\right)\left(cách\right)\)
=>Có tất cả 80640 cách
CM
18 tháng 8 2017
Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: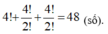 
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: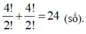 
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: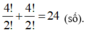 
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: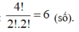 
Vậy có thể lập được 102 số thỏa mãn đề bài.
