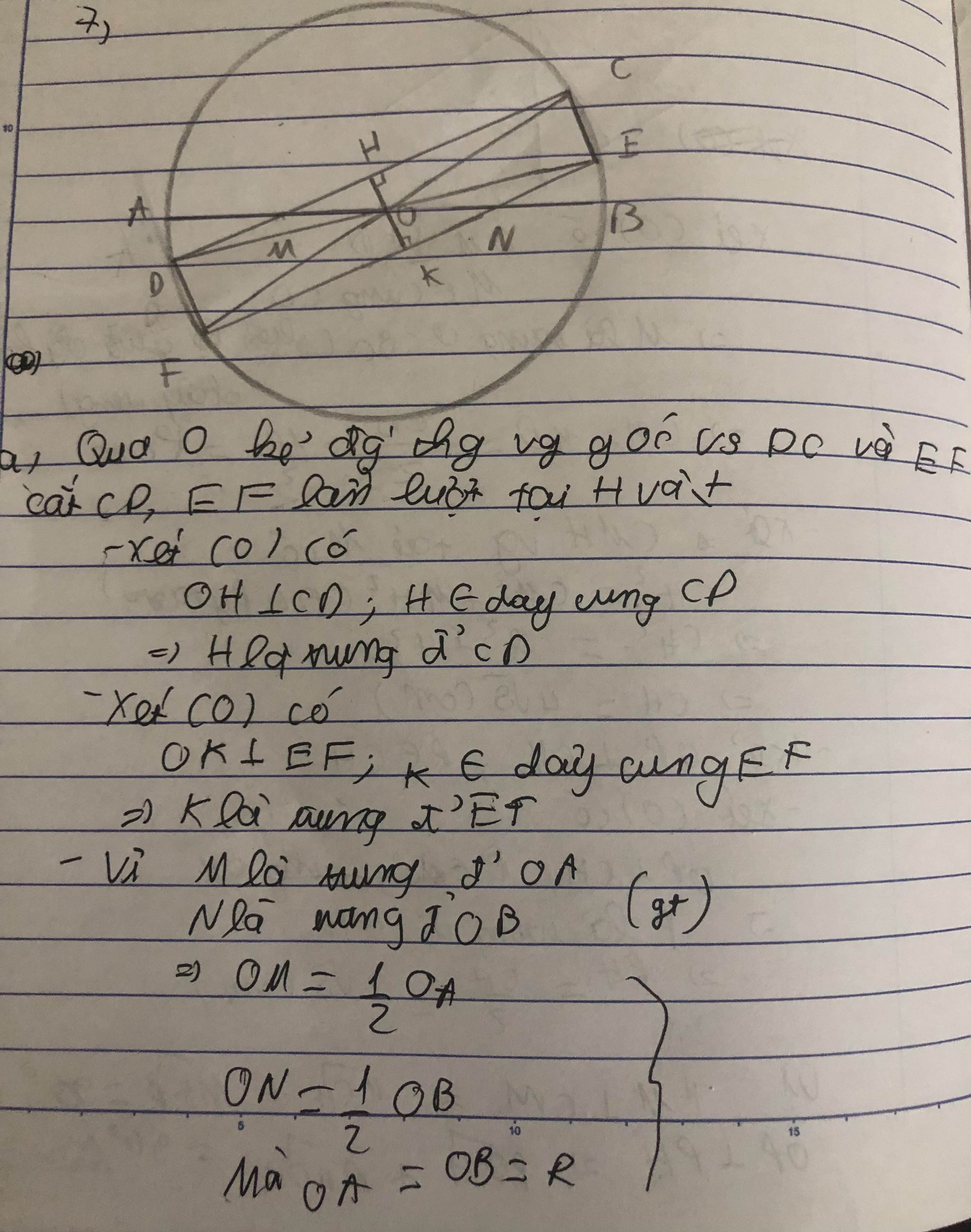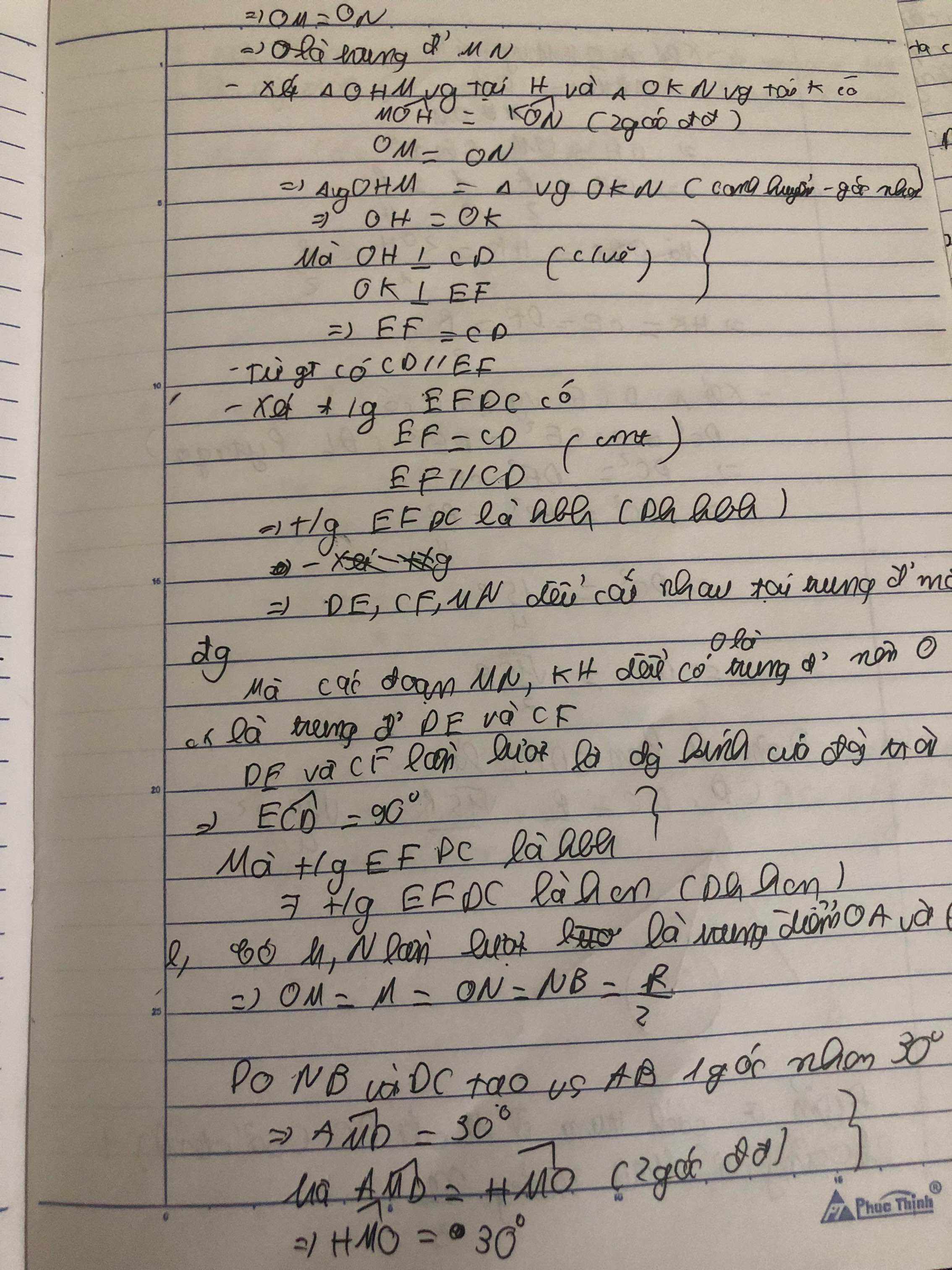Cho đường tròn $(O;R)$, đường kính $AB$. Gọi $M$, $N$ lần lượt là trung điểm của $OA$, $OB$. Qua $M$, $N$ lần lượt vẽ các dây $CD$ và $EF$ song song với nhau ($C$ và $E$ cùng nằm trên một nửa đường tròn đường kính $AB$).
a) Chứng minh tứ giác $CDFE$ là hình chữ nhật.
b) Giả sử $CD$ và $EF$ cùng tạo với $AB$ một góc nhọn \(30^o\). Tính diện tích hình chữ nhật $CDFE$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan