Bài 1: Tìm tất cả các số tự nhiên n sao cho số 28 + 211 + 2n là số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
0
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2022
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
TH
0
CN
1
27 tháng 5 2022
Do \(2n+1\) và \(3n+1\) là các số chính phương dương nên tồn tại các số nguyên dương a,b sao cho \(2n+1\)\(=a^2\) và \(3n+1=b^2\). Khi đó ta có:
\(2n+9=25.\left(2n+1\right)-16.\left(3n+1\right)=25a^2-16b^2=\left(5a-4b\right).\left(5a+4b\right)\)
Do \(2n+9\) là nguyên tố,\(5a+4b>1\) và \(5a+4b>5a-4b\) nên ta phải có \(5a-4b=1\), tức là: \(b=\dfrac{5a-1}{4}\)
\(\Rightarrow\) ta có: \(\left\{{}\begin{matrix}2n+1=a^2\left(1\right)\\3n+1=\dfrac{\left(5a-1\right)^2}{16}\left(2\right)\end{matrix}\right.\)
Từ (1) : \(2n+1=a^2\Rightarrow n=\dfrac{a^2-1}{2}\) và a > 1 ( do n>0)
Thay vào (2): \(\dfrac{3.\left(a^2-1\right)}{2}+1=\dfrac{\left(5a-1\right)^2}{16}\) => (a - 1).(a - 9) = 0
=> a = 9. Từ đó ta có n = 40
Vậy duy nhất một giá trị n thỏa mãn yêu cầu đề bài là : n = 40
TT
0
2 tháng 11 2016
a) \(4n-5⋮2n-1\)
\(\Rightarrow\left(4n-2\right)-3⋮2n-1\)
\(\Rightarrow2\left(2n-1\right)-3⋮2n-1\)
\(\Rightarrow-3⋮2n-1\)
\(\Rightarrow2n-1\in\left\{1;-1;3;-3\right\}\)
+) \(2n-1=1\Rightarrow2n=2\Rightarrow n=1\) ( chọn )
+) \(2x-1=-1\Rightarrow2n=0\Rightarrow n=0\) ( chọn )
+) \(2n-1=3\Rightarrow2n=4\Rightarrow n=2\) ( chọn )
+) \(2n-1=-3\Rightarrow n=-1\) ( loại )
Vậy \(n\in\left\{1;0;2\right\}\)
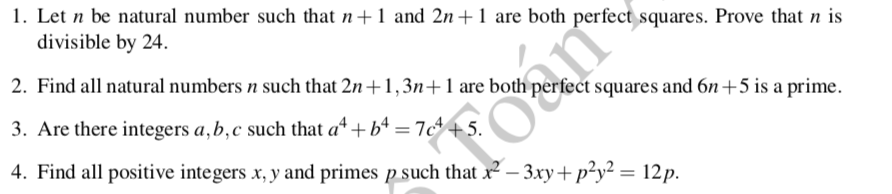
Ta có: A = 28 + 211 + 2n = 28.(1 + 23 + 2n-8) = (23)2.(1 + 2.22.1 + 24 +2n-8 - 24) = (23)2.((1 + 22)2 + 2n-8 - 24)
=> A là số chính phương <=> 2n-8=24=> n-8=4=> n=12
Ta có: A = 28 + 211 + 2n = 28.(1 + 23 + 2n-8) = (23)2.(1 + 2.22.1 + 24 +2n-8 - 24) = (23)2.((1 + 22)2 + 2n-8 - 24)
=> A là số chính phương <=> 2n-8=24=> n-8=4=> n=12