Cho tam giác ABC có góc A = 90 độ. Lấy điểm D trên cạnh AB, lấy E trên cạnh AC. Chứng minh DE < BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BN
1
Những câu hỏi liên quan
24 tháng 4 2020
Nối D và C ta có : E , AC lần lượt là hình chiếu của các hình xiên DE,DC trên đường thẳng AC
Mà AE < AC ( vì E thuộc cạnh AC )
=> DE < DC ( quan hệ giữa đường xiên và hình chiếu của nó )
Mặt khác : AD ;AB lần lượt là hình chiếu của các đường xiên DC,BC trên đường thẳng AB mà AD < AB ( D thuộc cạnh AB )
=> DC < BC ( quan hệ giữa đường xiên và hình chiếu của nó )
Ta có : DE < DC ; DC < BC => DE < BC ( đpcm )
21 tháng 2 2021
Đáp án:
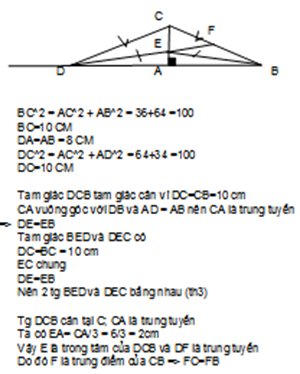
a) Vì ΔΔABC vuông tại A (Aˆ=90oA^=90o)
=> AB2+AC2=BC2AB2+AC2=BC2 (ĐL Pi-ta-go)
=> BC2=82+62=100BC2=82+62=100
=> BC=10BC=10cm
b) Vì AB = AD (gt)
mà A ∈∈ BD (gt)
=> A trung điểm BD (ĐN trung điểm)
=> CA trung tuyến BD (ĐN trung tuyến)
lại có: CA ⊥⊥ BD (AB ⊥⊥ AC do Aˆ=90oA^=90o)
=> ΔΔCBD cân tại C (dhnb)
=> BC = CD (ĐN ΔΔ cân)
và CA là phân giác của BCDˆBCD^ (t/c ΔΔ cân)
=> C1ˆ=C2ˆC1^=C2^ (ĐN tia p/g)
Xét ΔΔBEC và ΔΔDEC có:
BC = CD (cmt)
C1ˆ=C2ˆC1^=C2^ (cmt)
EC: cạnh chung
=> ΔΔBEC = ΔΔDEC (c.g.c)
c) Vì CE là trung tuyến của ΔΔBCD (cmt)
mà AEAC=26=13AEAC=26=13 (AE = 2cm, AC = 6cm)
=> E là trọng tâm ΔΔBCD (dhnb)
=> DE là trung tuyến ΔΔBCD (ĐN trọng tâm)
=> DE đi qua trung điểm của BC (ĐN trung tuyến)
CM
21 tháng 3 2018
+ ΔADE có ∠E1 là góc ngoài ⇒ ∠E1 > ∠A
Mà ∠A > 90o ⇒ ∠E1 > 90o
ΔCDE có ∠E1 tù ⇒ CD là cạnh lớn nhất ⇒ CD > DE (1)
+ Tương tự xét ΔADC có ∠D1 là góc ngoài
⇒ ∠D1 > ∠A ⇒ ∠D1 > 90o (vì ∠A > 90º)
ΔBDC có ∠D1 tù ⇒ BC là cạnh lớn nhất ⇒ BC > CD (2)
Từ (1) và (2) suy ra BC > DE.
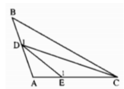
A=90 độ =>AEC là góc nhọn và CEB là góc tù
Xét tam giác CEB có CEB là góc tù =>BC sẽ là cạnh lớn nhất
=>BC>CE (1)
A=90 độ => ADE là góc nhọn và EDC là góc tù
Xét tam giác EDC có EDC là góc tù => EC sẽ là cạnh lớn nhất trong tam giác
=>EC>DE (2)
Từ (1) và (2) =>DE<BC (BC>CE mà CE lại >DE)