Cho đường tròn (O) đường kính AB. Từ điểm C thuộc đường tròn (O) kẻ CH vuông góc với AB ( C khác A và B; H thuộc AB). Đường tròn tâm C bán kính CH cắt đường tròn(O) tại D và E. Chứng minh DE đi qua trung điểm của CH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2020
a) Gọi N là trung điểm của OC
Ta có: ΔOHC vuông tại H(CH⊥AB tại H)
mà HN là đường trung tuyến ứng với cạnh huyền OC(N là trung điểm của OC)
nên \(HN=\dfrac{OC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(ON=CN=\dfrac{OC}{2}\)(N là trung điểm của OC)
nên HN=ON=CN(1)
Ta có: ΔOCI vuông tại I(OI⊥AC tại I)
mà IN là đường trung tuyến ứng với cạnh huyền OC(N là trung điểm của OC)
nên \(IN=\dfrac{OC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CN=ON=\dfrac{CO}{2}\)(N là trung điểm của CO)
nên IN=CN=ON(2)
Từ (1) và (2) suy ra NI=NO=NC=NH
hay I,O,C,H cùng thuộc một đường tròn(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔMAO vuông tại A có AI là đường cao ứng với cạnh huyền OM, ta được:
\(OI\cdot OM=OA^2\)
mà OA=R(A∈(O;R))
nên \(OI\cdot OM=R^2\)(đpcm)
Vì OM=2R và R=6cm nên \(OM=2\cdot6cm=12cm\)
Thay OM=12cm và R=6cm vào biểu thức \(OI\cdot OM=R^2\), ta được:
\(OI\cdot12=6^2=36\)
hay OI=3cm
Vậy: Khi OM=2R và R=6cm thì OI=3cm
20 tháng 6 2023
1: góc AKP+góc AHP=180 độ
=>AKPH nội tiếp
2: góc KAC=1/2*sđ cung KC
góc OMB=góc CBK(MH//CB)
=>góc OMB=góc KAC
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
a.
\(DH\perp AB\left(gt\right)\Rightarrow\widehat{DHB}=90^0\Rightarrow D;H;B\) cùng thuộc đường tròn đường kính DB
\(\widehat{AEB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O)) \(\Rightarrow\widehat{DEB}=90^0\)
\(\Rightarrow D;E;B\) cùng thuộc đường tròn đường kính DB
\(\Rightarrow\) Tứ giác BHDE nội tiếp đường tròn đường kính DB
b.
\(\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O))
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ \(\widehat{BAC}\))
Mà \(\widehat{ABC}=\widehat{AEC}\) (cùng chắn cung AC của (O)
\(\Rightarrow\widehat{ACH}=\widehat{AEC}\)
Xét hai tam giác ADC và ACE có: \(\left\{{}\begin{matrix}\widehat{ACH}=\widehat{AEC}\left(cmt\right)\\\widehat{CAD}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g.g\right)\Rightarrow\dfrac{AD}{AC}=\dfrac{CD}{EC}\Rightarrow AD.EC=CD.AC\)
c.
Cũng theo cmt \(\Delta ADC\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}\Rightarrow AD.AE=AC^2\)
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao CH:
\(BC^2=BH.BA\)
\(\Rightarrow AD.AE+BH.BA=AC^2+BC^2=AB^2=2022^2\)
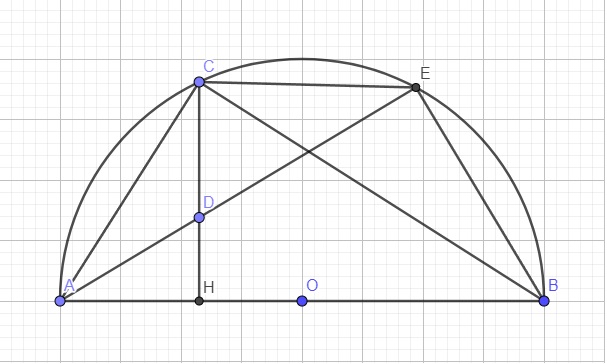
Gọi G là giao điểm của DE và CH. I là giao điểm của DE và OC. F là giao điểm của OC với (O)
Xét tam giác CGI và tam giác COH có:
\(\hept{\begin{cases}\widehat{HCO}chung\\\widehat{CIG}=\widehat{CHO}=90^0\end{cases}\Rightarrow\Delta CGI~\Delta COH\left(g-g\right)}\)
\(\Rightarrow\frac{CG}{CI}=\frac{CO}{CH}\)
\(\Rightarrow CG.CH=CO.CI\)
\(\Rightarrow2.CG.CH=2.CO.CI=CF.CI\)(1)
Áp dụng hệ thức lượng trong tam giác CEF vuông tại E có EI là đường cao ta có:
\(CF.CI=CE^2=CH^2\)(2)
Từ (1) và (2) \(\Rightarrow2.CG.CH=CH^2\)
\(\Rightarrow2CG=CH\)
\(\Rightarrow G\)là trung điểm của CH mà DE cắt CH tại G
\(\Rightarrow DE\)đi qua trung điểm của CH