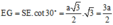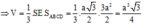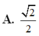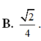Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong 2 mp vuông góc với nhau. Tính sin hợp bởi SA và mp(SCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
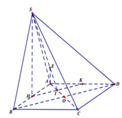
Gọi K là trung điểm CD \(\Rightarrow CD\perp\left(SIK\right)\)
\(\Rightarrow\widehat{ISK}\) là góc giữa SI và (SCD)
\(SI=\dfrac{a\sqrt{3}}{2}\) ; \(IK=a\)
\(SK=\sqrt{SI^2+IK^2}=\dfrac{a\sqrt{7}}{2}\)
\(sin\widehat{ISK}=\dfrac{IK}{SK}=\dfrac{2\sqrt{7}}{7}\)
HT
23 tháng 5 2016
a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
HT
23 tháng 5 2016
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
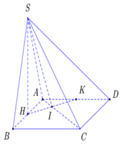
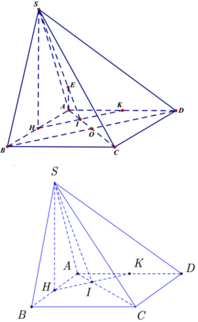
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)
