khi phân hủy bằng nhiệt 14,2 gam hỗn hợp X gồm CaCO3 và MgCO3 ta thu được chất rắn Y gồm CaO và MgO và 6,6 gam CO2. Tính thành phần % khối lượng các chất trong hỗn hợp X.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
10 tháng 7 2021
Áp dụng định luật BTKL :
\(m_{CO_2}=142-76=66\left(g\right)\)
\(n_{CO_2}=\dfrac{66}{44}=1.5\left(mol\right)\)
\(V_{CO_2}=1.5\cdot22.4=33.6\left(l\right)\)
\(n_{CaCO_3}=a\left(mol\right),n_{MgCO_3}=b\left(mol\right)\)
\(m_X=100a+84b=142\left(g\right)\left(1\right)\)
\(CaCO_3\underrightarrow{^{^{t^0}}}CaO+CO_2\)
\(MgCO_3\underrightarrow{^{^{t^0}}}MgO+CO_2\)
\(m_Y=56a+40b=76\left(g\right)\left(2\right)\)
\(\left(1\right),\left(2\right):a=1,b=0.5\)
\(\%CaO=\dfrac{56\cdot1}{76}\cdot100\%=73.68\%\)
\(\%MgO=100-73.68=26.32\%\)
10 tháng 7 2021
PTHH: \(CaCO_3\xrightarrow[]{t^o}CaO+CO_2\uparrow\)
a_______a_____a (mol)
\(MgCO_3\xrightarrow[]{t^o}MgO+CO_2\uparrow\)
b_______b_____b (mol)
Ta lập hệ phương trình: \(\left\{{}\begin{matrix}100a+84b=142\\56a+40b=76\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=0,5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CaO}=\dfrac{56}{76}\cdot100\%\approx73,68\%\\\%m_{MgO}=26,32\%\\V_{CO_2}=\left(1+0,5\right)\cdot22,4=33,6\left(l\right)\end{matrix}\right.\)
5 tháng 3 2022
Gọi số mol MgCO3, CaCO3 là a, b (mol)
=> 84a + 100b = 1,84 (1)
PTHH: MgCO3 --to--> MgO + CO2
a-------------------->a
CaCO3 --to--> CaO + CO2
b-------------------->b
=> a + b = \(\dfrac{0,448}{22,4}=0,02\) (2)
(1)(2) => a = 0,01 (mol); b = 0,01 (mol)
=> \(\left\{{}\begin{matrix}\%m_{MgCO_3}=\dfrac{0,01.84}{1,84}.100\%=45,65\%\\\%m_{CaCO_3}=\dfrac{0,01.100}{1,84}.100\%=54,35\%\end{matrix}\right.\)
28 tháng 9 2017
Na2CO3 không bị nhiệt phân, nên 2,24 lít khí sinh ra chính là CO2 do CaCO3 bị nhiệt phân theo phản ứng
Cách 1:
Áp dụng định luật bảo toàn khối lượng ta có:
m X = m c h ấ t r ắ n + m C O 2 = 11,6 + 0,1.44 = 16 (gam)
Vậy phần trăm khối lượng của CaCO3 trong hỗn hợp X là:
Cách 2:
Ta có:
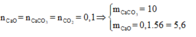
Hỗn hợp rắn thu được gồm CaO và Na2CO3
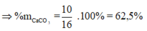
Đáp án D
15 tháng 12 2019
Đáp án D
nCO2= nCaCO3 = 0,15 mol
ð mCaCO3 = 15 gam
mX= mrắn + mCO2
= 17,4+ 0,15.44=24 gam
%mCaCO3= (15:24).100%=62,5%
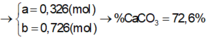
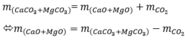
Gọi số mol CaCO3, MgCO3 là a, b (mol)
=> 100a + 84b = 14,2 (1)
\(n_{CO_2}=\dfrac{6,6}{44}=0,15\left(mol\right)\)
PTHH: CaCO3 --to--> CaO + CO2
a-------------------->a
MgCO3 --to--> MgO + CO2
b---------------------->b
=> a + b = 0,15
=> a = 0,1; b = 0,05
=> \(\left\{{}\begin{matrix}\%m_{CaCO_3}=\dfrac{100.0,1}{14,2}.100\%=70,42\%\\\%m_{MgCO_3}=\dfrac{0,05.84}{14,2}.100\%=29,58\%\end{matrix}\right.\)
\(n_{CO_2}=\dfrac{6,6}{44}=0,15mol\)
\(CaCO_3\underrightarrow{t^o}CO_2+CaO\)
\(x\) \(\rightarrow\) \(x\)
\(MgCO_3\underrightarrow{t^o}MgO+CO_2\)
\(y\) \(\rightarrow\) \(y\)
\(\Rightarrow\left\{{}\begin{matrix}100x+84y=14,2\\x+y=0,15\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0,1\\y=0,05\end{matrix}\right.\)
\(\%m_{CaCO_3}=\dfrac{0,1\cdot100}{14,2}\cdot100\%=70,42\%\)
\(\%m_{MgCO_3}=100\%-70,42\%=29,57\%\)