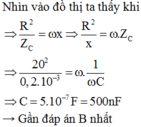Một xạ thủ bắn súng. Số điểm đc sau mỗi lần bán đc ghi vào bảng sau đây (lần bắn nào cx có điểm). Bt điểm trung bình cộng bằng 8,75. Hãy tìm giá trị của a và bĐiểm(x) 7...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TA

Trâm Anh

17 tháng 2 2022

Một xạ thủ bắn súng. Số điểm đc sau mỗi lần bán đc ghi vào bảng sau đây (lần bắn nào cx có điểm). Bt điểm trung bình cộng bằng 8,75. Hãy tìm giá trị của a và bĐiểm(x) 7 8 9 10 N=32Tần số(n) a 9 b 9 ...

0

Những câu hỏi liên quan

A

Angle

25 tháng 4 2015 - olm

Bài 1 Lớp 5A có số học sinh giỏi bằng 2/3 số học sinh khá , số học sinh khá bằng 3/4 số học sinh trung bình, không có học sinh xếp loại yếu , kém . Hãy tính sô học sinh mỗi loại biết số học sinh của lớp 5A là 1 số lớn hơn 30 và bé hơn 45Bài 2 Trong kỳ thi học kỳ 2 số điểm 10 của tổ 1 bằng 1/2 số điểm 10 của 3 tổ còn lại. Số điểm 10 của tổ 2 bằng...

0

PT

Pham Trong Bach

3 tháng 8 2017

Hai xạ thủ bắn mỗi người một viên đạn vào bia, biết xác suất bắn trúng vòng 10 của xạ thủ thứ nhất là 0,75 và của xạ thủ thứ hai là 0,85. Tính xác suất để có ít nhất một viên trúng vòng 10 ?

A. 0,9625

B. 0,325

C. 0, 6375

D. 0,0375

#Toán lớp 11

1

CM

Cao Minh Tâm

3 tháng 8 2017

Gọi A là biến cố: “có ít nhất một viên trúng vòng 10.”

⇒ A ¯ là biến cố: “Không viên nào trúng vòng 10.”

Gọi X là biến cố người thứ 1 bắn trúng vào10: P ( X ) = 0 , 75 ; P ( X ¯ ) = 1 − 0 , 75 = 0 , 25

Gọi Y là biến cố người thứ 2 bắn trúng vào10: P ( Y ) = 0 , 85 ; P ( Y ¯ ) = 1 − 0 , 85 = 0 , 15

Ta có; A ¯ = X ¯ . Y ¯ ; hai biến cố X ¯ ; Y ¯ là hai biến cố độc lập với nhau nên ta có:

P ( A ¯ ) = P ( X ¯ ) . P ( Y ¯ ) = 0 , 25. 0 , 15 = 0 , 0375

Do đó, xác suất của biến cố A là:

P ( A ) = 1 − P ( A ¯ ) = 1 − 0 , 0375 = 0 , 9625

Chọn đáp án A.

B

bong

31 tháng 3 2016 - olm

Bài 4 : Cho phân số tối giản a/b , biết nếu cộng vào cả tử và mẫu cùng mẫu số của phân số đã cho sẽ thu được phân số mới có giá trị bằng 4 lần giá trị phân số ban đầu . Hãy tìm phân số a/b

0

NT

Nguyễn Thị Anh Thư

9 tháng 10 2017 - olm

Trong thực tế, khi đếm hay đo các đại lượng, ta thường chỉ đc các số gần đúng. Để có thể thu đc kết quả có nhiều khả năng sát số đúng nhất, ta thường phai đếm hay đo nhiều lần rồi tính trung bình cộng của các số gần đúng tìm đc. Háy tìm giá trị có nhiều khả năng sát số đúng nhất của số đo chiều dài lớp học của em sau khi đo 5 lần...

2

ND

nguyễn đức vượng 3

9 tháng 10 2017

k mk nhé

NT

Nguyễn Thị Anh Thư

9 tháng 10 2017

Cảm ơn bạn !!!!!!!

NH

Ngọc Hưng

27 tháng 3 2022

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của SC. Một mặt phẳng (P) chứa AM và lần lượt cắt các cạnh SB, SD tại các điểm B', D' khác S. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức T = \(\dfrac{SB'}{SB}+\dfrac{SD'}{SD}\) . Khi đó M + m...

#Toán lớp 11

1

KB

Khôi Bùi

28 tháng 3 2022

Gọi O là tâm của hình bình hành ABCD; G = SO∩AM ⇒ G là trọng tâm ΔSAC ⇒ SG/SO = 2/3 ⇒ G cũng là trọng tâm ΔSBD

G ∈ AM ⊂ (P); G ∈ SO ⊂ (SBC) (1)

B' ∈ (P) và B' ∈ SB ⊂(SBC) (2)

D' ∈ (P) và D' ∈ SD ⊂(SBC) (3)

Từ (1); (2); (3) ⇒ G; B'; D' ∈ giao tuyến của (P) và (SBC)

Trong (SBC) vẽ BM//SO//DN (M, N ∈ B'D') ⇒ OG là đường trung bình của hình thang BDNM

⇒ BM + DN = 2OG = SG

Ta có :

x = SB/SB' = (SB' + BB')/SB' = 1 + BB'/SB' = 1 + BM/SG

y = SD/SD' = (SD' + DD')/SD' = 1 + DD'/SD' = 1 + DN/SG

⇒ x + y = 2 + (BM + DN)/SG = 2 + 1 = 3

1/x + 1/y = SB'/SB + SD'/SD = a/b

⇒ 3a/b = (x + y)(1/x + 1/y) ≥ 2√(xy).2√(1/xy) = 4

⇒ u = a/b ≥ 4/3 tối giản ⇒ GTNN của u = 4/3 xảy ra khi x = y ⇔ SB'SB' = SD/SD' ⇔ B'D'//BD

HD

Hoàng Đức Long

24 tháng 7 2018

Đặt một điện áp u = U 0 cos(ωt)(V) vào hai đầu đoạn mạch gồm điện trở R, tụ điện có điện dung C và dây thuần cảm hệ số tự cảm L mắc theo đúng thứ tự trên. Trong đó tụ điện C không thay đổi, R và L thay đổi được. Ứng với mỗi giá trị R, gọi L 1 , L 2 lần lượt là giá trị L để u ...

#Vật lý lớp 12

1

VT

Vũ Thành Nam

24 tháng 7 2018

Chọn đáp án B

+ Khi L = L 1 thì U R C vuông pha với u nên:

+ Khi L = L 2 thì mạch có cộng hưởng nên

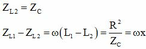
+ Nhìn vào đồ thị ta thấy khi

HD

Hoàng Đức Long

25 tháng 11 2017

Đặt một điện áp u = U 0 cos ω t (V) vào hai đầu đoạn mạch gồm điện trở R, tụ điện có điện dung C và dây thuần cảm hệ số tự cảm L mắc theo đúng thứ tự trên. Trong đó tụ điện C không thay đổi, R và L thay đổi được. Ứng với mỗi giá trị R, gọi L 1 , L 2 lần lượt là giá trị L để u R ...

1

VT

Vũ Thành Nam

25 tháng 11 2017

Chọn đáp án B

PT

Pham Trong Bach

29 tháng 8 2019

Cho bảng phân bố tần số sau: Lớp [20;25) [25;30) [30;35) [35;40) [40;45) Cộng Tần số 2 7 15 8 3 35 a) Trong các giá trị sau đây, giá trị nào gần nhất với số trung bình của bảng số liệu trên? A. 31,5 B. 32 C. 32,5 D....

#Toán lớp 10

1

CM

Cao Minh Tâm

29 tháng 8 2019

Ta bổ sung thêm một cột ghi giá trị đại diện của mỗi lớp:

Lớp	[20;25)	[25;30)	[30;35)	[35;40)	[40;45)	Cộng
Tần số	2	7	15	8	3	35
Giá trị đại diện	22,5	27,5	32,5	37,5	42,5

Áp dụng công thức ta tìm được số trung bình:

x = 22 , 5 . 2 + 27 , 5 . 7 + 32 , 5 . 15 + 37 , 5 . 8 + 42 , 5 . 3 35 ≈ 32 , 93

Đáp án là D.

LK

Lý Kiều Hoàng Oanh

23 tháng 9 2016 - olm

trong một giải bóng đá nhi đồng có 6 đội tham gia bóng đá tham gia thi đấu theo thể thức vòng tròn một lược. sau mỗi trận đấu, đội thắng được tính 3 điểm, đội hòa được tính 1 điểm, đội thua không có điểm. các đội xếp hạng dựa trên tổng số điểm. kết thúc giải, ban tổ chức nhận thấy rằng không có trận đấu hòa, các đội xếp...

0