Cho a gam dung dịch HCl C% tác dụng hết với một lượng hỗn hợp 2 kim loại Na dư và K dư, thấy khối lượng H2 bay ra là 0,05a gam.Tìm C%.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
25 tháng 4 2022
\(2Na+H_2SO_4\rightarrow Na_2SO_4+H_2\)
\(Zn+H_2SO_4\rightarrow ZnSO_4+H_2\)
\(nH_2=\dfrac{0,05}{2}=0,025\left(mol\right)\)
=>\(nH_2SO_4=0,025\left(mol\right)\)
=> \(mH_2SO_4=0,025.98=2,45\left(g\right)\)
- muốn tính C% H2SO4 cần thêm dữ kiện .
20 tháng 3 2017
Đặt a=100 (g)
Theo đề ta có các PTHH:
\(2K+H_2SO_4\xrightarrow[]{}K_2SO_4+H_2\)(1)
\(Mg+H_2SO_4\xrightarrow[]{}MgSO_{4_{ }}+H_2\)(2)
\(2K+2H_2O\xrightarrow[]{}2KOH+H_2\) (3)
(K dùng dư nên cũng tác dụng với H2O)
Theo đề: \(m_{H_2SO_4}=100\times A\%=A\left(g\right)\)
=> \(n_{H_2SO_4}=\dfrac{A}{98}\left(mol\right)\)
\(n_{H_2}=\dfrac{0,05\times100}{2}=2,5\left(mol\right)\)
\(m_{H_2O}=m_{ddH_2SO_4}-m_{H_2SO_4}=100-A\left(g\right)\)
=>\(n_{H_2O}=\dfrac{100-A}{18}\left(mol\right)\)
Theo PTHH(1),(2),(3) ta có:
\(n_{H_2}=n_{H_2SO_4}+\dfrac{1}{2}\times n_{H_2O}=\dfrac{A}{98}+\dfrac{1}{2}\times\dfrac{100-A}{18}=\dfrac{A}{98}+\dfrac{100-A}{36}=2,5\left(mol\right)\)
=> A=15,8
Vậy nồng độ dung dịch H2SO4 là 15,8%
20 tháng 3 2017
\(PTHH:\)
\(H_2SO_4+2K--->K_2SO_4+H_2\) \((1)\)
\(H_2SO_4+Mg--->MgSO_4+H_2\) \((2)\)
\(mH_2SO_4=\)\(\dfrac{C\%H_2SO_4.mddH_2SO_4}{100}\)\(=\)\(\dfrac{Aa}{100} (g)\)
\(=> nH_2SO_4=\dfrac{Aa}{100}.98=0,98Aa (mol)\)
\(nH_2=\dfrac{0,05a}{2} = 0,025a (mol)\)
Theo PTHH (1) và (2) \(nH_2SO_4=nH_2\)
\(<=> 0,98Aa=0,025a\)
\(<=> 0,98A=0,025\)
\(<=> A=39,2 \)
Vậy nồng độ phần trăm của dung dich \(H_2SO_4\) cần tìm là \(39,2\%\)
22 tháng 3 2019
Đáp án B
Chọn m = 100 (gam). Vì kim loại dùng dư nên sau khi axit hết, K tác dụng với nước cũng sinh H2.
30 tháng 12 2021
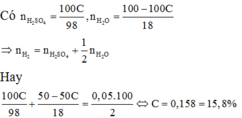
\(m_{Mg}=1,2\left(g\right)\)
=> \(n_{Mg}=\dfrac{1,2}{24}=0,05\left(mol\right)\)
\(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
PTHH: Mg + 2HCl --> MgCl2 + H2
____0,05--------------------->0,05
2Al + 6HCl --> 2AlCl3 + 3H2
\(\dfrac{1}{30}\)<--------------------0,05
=> \(m_{Al}=\dfrac{1}{30}.27=0,9\left(g\right)\)
=> \(\left\{{}\begin{matrix}\%Al=\dfrac{0,9}{0,9+1,2}.100\%=42,857\%\\\%Mg=\dfrac{1,2}{0,9+1,2}.100\%=57,143\%\end{matrix}\right.\)
H
13 tháng 2 2023
$m_{H_2SO_4} = a.C\%(gam) \Rightarrow n_{H_2SO_4} = \dfrac{a.C\%}{98}$
$m_{H_2O\ trong\ dd\ axit} = a - a.C\% \Rightarrow n_{H_2O} = \dfrac{a - a.C\%}{18}$
$2Na + H_2SO_4 \to Na_2SO_4 + H_2$
$Mg + H_2SO_4 \to MgSO_4 + H_2$
$2Na + 2H_2O \to 2NaOH + H_2$
Theo PTHH :
$n_{H_2} = n_{H_2SO_4} + \dfrac{1}{2}n_{H_2O}$
$\Rightarrow \dfrac{0,05a}{2} = \dfrac{a.C\%}{98} + \dfrac{1}{2}.\dfrac{a - a.C\%}{18}$
$\Rightarrow C\% = 0,158 = 15,8\%$
B
18 tháng 2 2022
2Na+2H2O->2NaOH+H2
x-------------------x----------0,5x mol
Ba+2H2O->Ba(OH)2+H2
y---------------------y----------y mol
aTa có :)\(\left\{{}\begin{matrix}23x+137y=2,06\\0,5x+y=0,025\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0,03\\y=0,01\end{matrix}\right.\)
=>mbazo=0,03.40+0,01.171=2,91g
=>m Na=0,03.23=0,69g
=>m Ba=0,01.137=1,27g
\(n_{H_2} = \dfrac{0,05a}{2} = 0,025a(mol)\\ n_{HCl} = \dfrac{a.C\%}{36,5} = \dfrac{a.C}{3650}(mol)\\ n_{H_2O} = \dfrac{a-a.C\%}{18}(mol)\)
\(Na + HCl \to NaCl + \dfrac{1}{2}H_2\\ K + HCl \to KCl + \dfrac{1}{2}H_2\\ Na + H_2O \to NaOH + \dfrac{1}{2}H_2\\ K + H_2O \to KOH + \dfrac{1}{2}H_2\\ 2n_{H_2} = n_{HCl} + n_{H_2O}\\ \Rightarrow 0,025a.2 = \dfrac{a.C}{3650} + \dfrac{a-a.C\%}{18}\)
\(\Leftrightarrow 0,05 = \dfrac{C}{3650} + \dfrac{1-0,01C}{18}\\ \Rightarrow C = 19,72\)