Chứng minh rằng : nếu ba số a;a+k ; a+2k nguyên tố lớn hơn 3 thì k chia hết cho 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 12 2019
Để ý rằng
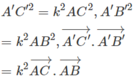
Ta có:
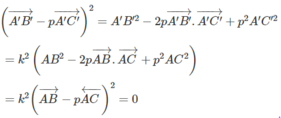
Từ đó suy ra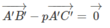 
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
CM
16 tháng 5 2018
Do a, a + k, a + 2k đều là nguyên tố lớn hơn 3 nên đều là số lẻ và không chia hết cho 3.
• Vì a và a + k cùng lẻ nên a + k - a = k ⋮ 2. (1)
• Vì a, a + k, a + 2k đều không chia hết cho 3 nên khi chia cho 3 ít nhất hai số có cùng số dư, khi đó:
+ Nếu a và a + k có cùng số dư, thì suy ra: (a+k) - a = k ⋮ 3
+ Nếu a + k và a + 2k có cùng số dư, thì suy ra: (a+2k )- (a+k)= k ⋮ 3+ Nếu a và a + 2k có cùng số dư, thì suy ra:
( a + 2k ) - a = 2k 3 nhưng (2,3) = 1 nên k 3
Vậy, ta luôn có k chia hết cho 3 (2)
Từ (1),(2) và do (2,3)=1 ta suy ra k ⋮ 6, đpcm.
Nhận xét: Trong lời giải trên, ta đã định hướng được rằng để chứng minh k ⋮ 6 thì cần chứng minh k ⋮ 2 và k ⋮ 3 và ở đó:
• Việc chứng minh k ⋮ 2 được đánh giá thông qua nhận định a, a + k,a + 2k đều là nguyên tố lẻ hơn kém nhau k đơn vị.
• Việc chứng minh k ⋮ 3 được đánh giá thông qua nhận định “ba số lẻ không chia hết cho 3 thì có ít nhất hai số có cùng số dư” và như vậy hiệu của hai số đó sẽ chia hết cho 3.
CM
23 tháng 2 2018
Giả sử p ≠ 0 ta có:
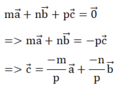
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
HK
0
VD
2
CM
9 tháng 1 2018
Gọi 3 số đó là a - d, a, a + d rồi áp dụng tính chất của cấp số cộng và cấp số nhân.
Câu hỏi của Nguyễn Anh Kim Hân - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo nhé!