Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1/3. Tìm n.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
CM
19 tháng 9 2017
Đáp án C
Phương pháp: Số tam giác vuông bằng số đường kính của đường tròn có đầu mút là 2 đỉnh của đa giác (H) nhân với (2n – 2) tức là số đỉnh còn lại của đa giác.
Cách giải: Số phần tử của không gian mẫu: n Ω = C 2 n 3
Tam giác vuông được chọn là tam giác chứa một cạnh là đường kính của đường tròn tâm O.
Đa giác đều 2n đỉnh chứa 2n đường chéo là đường kính của đường tròn tâm O, mỗi đường kính tạo nên 2n – 2 tam giác vuông.
Do đó số tam giác vuông trong tập S là: 
Xác suất chọn một tam giác vuông trong tập S :
CM
6 tháng 9 2018
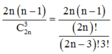
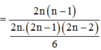
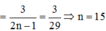
Số phần tử của tập X là C 4 n 3
Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O.
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4n-2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
Từ giả thiết suy ra P A = C 2 n 1 . C 4 n - 2 1 C 4 n 3 = 1 13 ⇒ n = 10
Đáp án C
CM
2 tháng 3 2017
Đáp án C
Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O .
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4 n - 2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
CM
16 tháng 4 2017
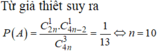
Chọn B
Các số tự nhiên của tập X có dạng a b c d e ¯ , suy ra tập X có 9. 10 4 số. Lấy từ tập X ngẫu nhiên hai số có C 90000 2 số.
Vì 
có 25 số.
Suy ra số tự nhiên có năm chữ số chia hết cho 4 là 9.10.10.25 = 22500 số.
Số tự nhiên có năm chữ số không chia hết cho 4 là 9.10.10.75 = 67500 số.
Vậy xác suất để ít nhất một số chia hết cho 4 là: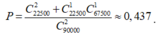 
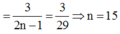
Mọi người ơi,đây là olm beta à.
đúng rồi bn ơi