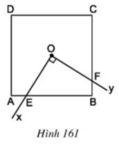
Cho hình vuông ABCD có tâm là O. Vẽ tia Ox cắt BC ở E, vẽ tia Oy cắt AB ở F sao cho góc xOy bằng 90 độ ( E không trùng với B và C, F không trùng với với A và B). Tính tỉ số diện tích giữa tứ giác OEBF và hình vuông ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


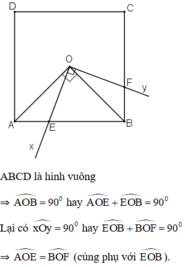
ABCD là hình vuông
\(\Rightarrow\widehat{AOB}=90^o\)hay \(\widehat{AOE}+\widehat{EOB}=90^o\)
Ta lại có : \(\widehat{xOy}=90^o\)hay \(\widehat{EOB}+\widehat{BOF}=90^o\)
\(\Rightarrow\widehat{AOE}=\widehat{BOF}\)( cùng phụ với \(\widehat{EOB}\))
+) Xét 2 tam giác : AOE và BOF , có :
OA = OB
\(\widehat{OAE}=\widehat{OBF}\left(=90^o\right)\)
\(\widehat{AOE}=\widehat{BOF}\left(cmt\right)\)
\(\Rightarrow\Delta AOE=\Delta BOF\left(g-c-g\right)\)
\(\Rightarrow S_{AOE}=S_{BOF}\)
\(\Rightarrow S_{AOE}+S_{OEB}=S_{BOF}+S_{OEB}\)
hay \(S_{AOB}=S_{OEBF}\)
Mà \(S_{AOB}=\frac{1}{2}S_{ABCD}=\frac{a^2}{4}\)
\(\Rightarrow S_{OEBF}=\frac{a^2}{4}\)