Tổng các nghiệm của phương trình: (x-6)⁴ + (x-8)⁴ = 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 5 2019
Ta có: x 2 + 4 x + 6 x 2 − 16 = 0
⇔ x 2 + 4 = 0 x + 6 = 0 x 2 − 16 = 0 ⇔ x 2 = − 4 < 0 V N x = 6 x = ± 4
Tổng các nghiệm của phương trình là: -6 + 4 + (-4) = -6
Đáp án cần chọn là D
N
1
PT
1
28 tháng 6 2023
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
PT
1
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
CM
31 tháng 1 2017
Đáp án D
Phương trình tương đương với 4 4 x + 1 4 x = 4 ( m + 1 ) 2 x - 1 2 x + 16 - 8 m
⇔ 4 x + 1 4 x = ( m + 1 ) 2 x - 1 2 x + 4 - 2 m (1)
Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t (x) luôn đồng biến trên [0;1]. Suy ra m i n x ∈ [ 0 ; 1 ] t ( x ) = t ( 0 ) = 0 và m a x x ∈ [ 0 ; 1 ] t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng: t 2 + 2 = ( m + 1 ) t + 4 - 2 m ⇔ t 2 - ( m + 1 ) t + 2 m = 0
⇔ ( t - 2 ) t + 1 - m = 0 ⇔ t = 2 ∉ 0 ; 3 2 t = m - 1
Phương trình (1) có nghiệm x ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm
t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.
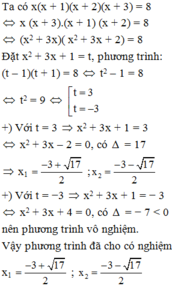
\(\left(x-6\right)^4+\left(x-8\right)^4=16\)
\(\Leftrightarrow\left(x-6\right)^4+\left(x-8\right)^4-16=0\)
\(\Leftrightarrow\left(x-8\right)\left[\left(x-6\right)^3+\left(x-6\right)^2.2+\left(x-6\right).2^2+2^3\right]+\left(x-8\right)^4=0\)
\(\Leftrightarrow\left(x-8\right)\left[\left(x-6\right)^3+\left(x-6\right)^2.2+\left(x-6\right).2^2+2^3+\left(x-8\right)^3\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[x^3-3x^2.6+3x.6^2-6^3+\left(x^2-12x+36\right).2+4x-24+8+x^3-3x^2.8+3x.8^2-8^3\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[x^3-18x^2+108x-216+2x^2-24x+72+4x-24+8+x^3-24x^2+192x-512\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[2x^3-40x^2+280x-672\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[x^3-20x^2+140x-336\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[x^3-6x^2-14x^2+84x+56x-336\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left[x^2\left(x-6\right)-14x\left(x-6\right)+56\left(x-6\right)\right]=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-6\right)\left(x^2-14x+56\right)=0\)
\(\Leftrightarrow x-8=0\) hay \(x-6=0\) hay \(x^2-14x+56=0\)
\(\Leftrightarrow x=8\) hay \(x=6\) hay \(\left(x-7\right)^2+7=0\) (vô nghiệm).
\(\Leftrightarrow S=\left\{8;6\right\}\).
-Vậy tổng các nghiệm của phương trình là 14.