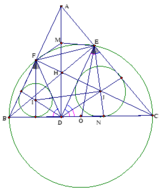
Cho tam giác ABC có đường cao AH, biết góc BCA < góc ABC < góc CAB < 900. Gọi đường tròn (O) tâm O là đường tròn ngoại tiếp tam giác ABC. Gọi I là tâm đường tròn nội tiếp tam giác ABC. Gọi D là giao điểm của tia AI với đường tròn (O), biết D khác A. Gọi E và F lần lượt là giao điểm của đường thẳng AH với hai đường thẳng BD và CI, biết E nằm giữa hai điểm B và D.
1) Chứng minh BH = AB.cos góc ABC. Suy ra BC = AB.cos góc ABC + AC.cos góc BCA.
2) Chứng minh bốn điểm B, E, I, F cùng thuộc một đường tròn.
3) Xác định tâm đường tròn ngoại tiếp tam giác IBC.