cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D sao cho AB = BD. Trên tia đối của tia CB lấy điểm E sao cho AC = CE. Chứng minh DE = AB+AC+BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

5 tháng 3 2022
Bài 8:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
b: ta có: ΔABD=ΔACE
nên \(\widehat{ADB}=\widehat{AEC}\)

14 tháng 4 2021
1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có
AB=AD(gt)
AC=AE(gt)
Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
14 tháng 4 2021
2) Xét ΔABD có AB=AD(gt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)
nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)
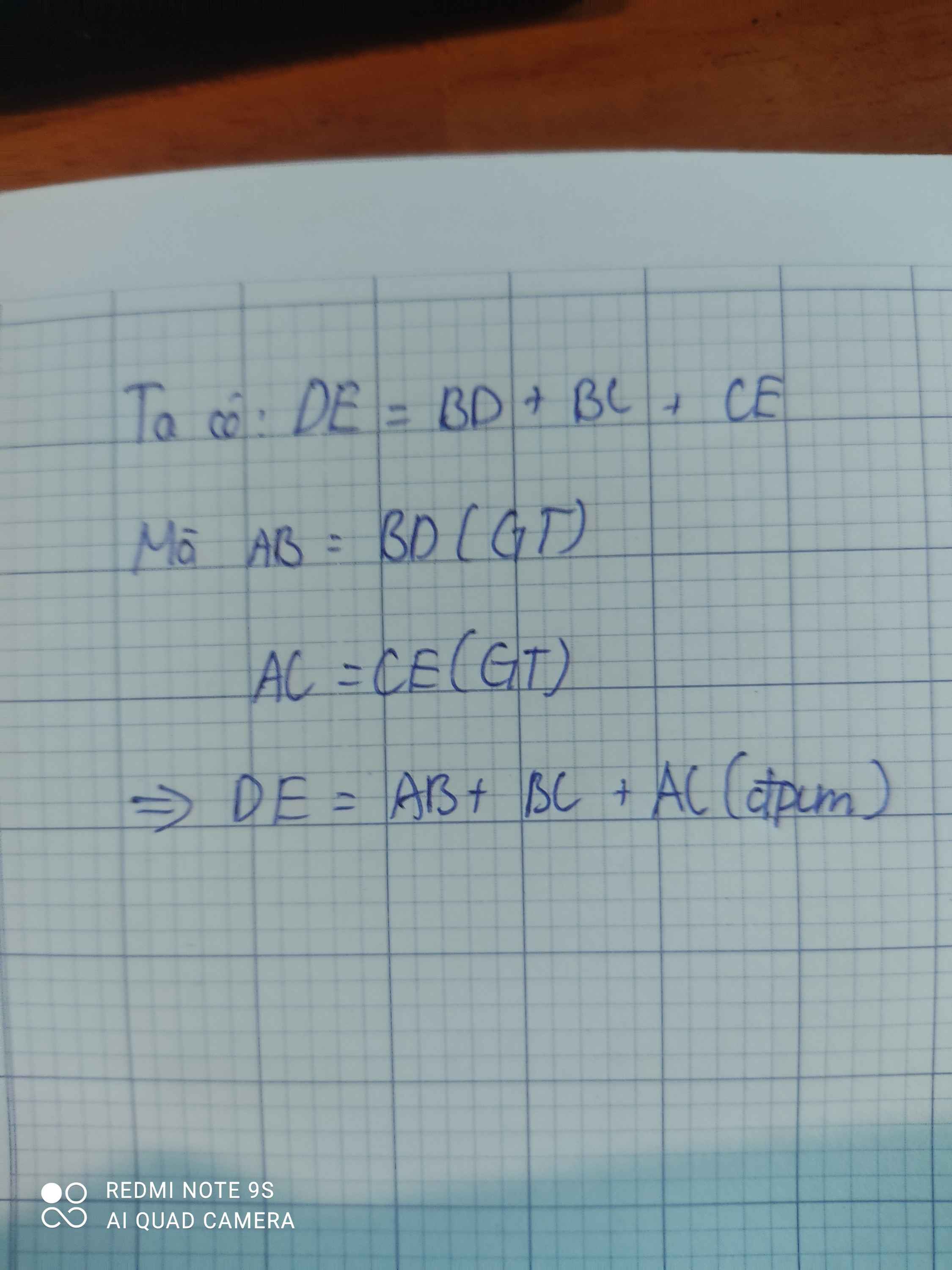
DE=DB+BC+CE
nên DE=AB+AC+BC
Vì tam giác ABC cân tại A
⇒ \(AB=AC\)
mà \(\left\{{}\begin{matrix}BD=AB\\AC=CE\end{matrix}\right.\)
\(\Rightarrow AB=AC=BD=CE\)
Ta có:
\(DE=BD+BC+CE\)
\(=AB+AC+BC\)(đpcm)