Cho góc xOy có Oz là tia phân giác, M là điểm bất kì thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D
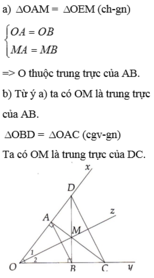
a) Chứng minh ^AOM=^BOM. Từ đó suy ra OM là đường trung trực của đoạn thẳng AB
b) Tam giác DMC là tam giác gì? Vì sao?
c) Chứng minh DM+AM<DC
Bạn nào làm được thì làm gấp hộ mình cái nhé.

Mới lớp 5